Question

【题目】已知函数f（x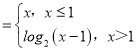），则函数y＝f（f（x））﹣1的所有零点构成的集合为_____.

Answer 1

【答案】{1，3，9}

【解析】

根据零点定义解方程，求出零点．

函数y＝f[f（x）]﹣1的零点，即求方程f[f（x）]﹣1＝0的解，利用换元法进行求解即可.

解：由y＝f（f（x））﹣1＝0得f（f（x））＝1，

设t＝f（x），则等价为f（t）＝1，

当x≤1时，由f（x）＝x＝1得x＝1，

当x＞1时，由f（x）＝log2（x﹣1）＝1得x＝3，

即t＝1或t＝3，

当x≤1时，由f（x）＝x＝1，得x＝1；由f（x）＝x＝3，得x＝3（舍），故此时x＝1；

当x＞1时，由f（x）＝log2（x﹣1）＝1得x＝3；由f（x）＝log2（x﹣1）＝3，得x＝9，

综上x＝1，或x＝3或x＝9．

所以函数y＝f[f（x）]﹣1的所有零点所构成的集合为：{1，3，9}

故答案为：{1，3，9}.