题目内容
(本题满分14分) 已知F1、F2是椭圆 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足 (
( 是坐标原点),
是坐标原点),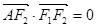 ,若椭圆的离心率等于
,若椭圆的离心率等于 .
.
(Ⅰ)求直线AB的方程;
(Ⅱ)若三角形ABF2的面积等于4 ,求椭圆的方程;
,求椭圆的方程;
(Ⅲ)在(Ⅱ)的条件下,椭圆上是否存在点M,使得三角形MAB的面积等于8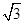 .
.
 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足 (
( 是坐标原点),
是坐标原点),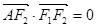 ,若椭圆的离心率等于
,若椭圆的离心率等于 .
. (Ⅰ)求直线AB的方程;
(Ⅱ)若三角形ABF2的面积等于4
 ,求椭圆的方程;
,求椭圆的方程;(Ⅲ)在(Ⅱ)的条件下,椭圆上是否存在点M,使得三角形MAB的面积等于8
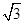 .
.(Ⅰ)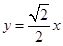
(Ⅱ)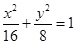
(Ⅲ)椭圆上不存在点M使得三角形MAB的面积等于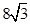
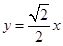
(Ⅱ)
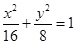
(Ⅲ)椭圆上不存在点M使得三角形MAB的面积等于
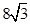
本试题主要是考查了直线方程的求解,以及椭圆方程的求解和三角形面颊的综合运用。
(1)根据已知的向量关系,直线过原点,并且向量的垂直关系可以得到点A的坐标,然后将点A的坐标代入椭圆方程中可知得到直线的方程。
(2)连结AF1、BF1、AF2、BF2,由椭圆的对称性可知,参数a,bc的关系式,进而得到椭圆的方程。
(3)由于由(Ⅱ)可以求得|AB|=2|OA|
假设在椭圆上存在点M使得三角形MAB的面积等于8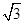
设点M到直线AB的距离为d,则应有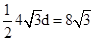
利用三角形的面积公式得到。
解:(Ⅰ)由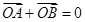 知,直线AB经过原点,又由
知,直线AB经过原点,又由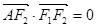 知
知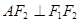 ,因为椭圆的离心率等于
,因为椭圆的离心率等于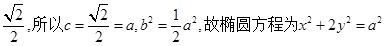 ……2分
……2分
设A(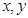 ),由
),由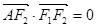 知
知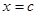
∴A(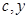 ),代入椭圆方程得
),代入椭圆方程得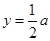 ∴A(
∴A(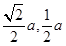 ),故直线AB的斜率
),故直线AB的斜率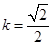
因此直线AB的方程为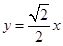 ……………4分
……………4分
(Ⅱ)连结AF1、BF1、AF2、BF2,由椭圆的对称性可知
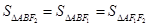 ,所以
,所以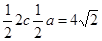 ……………6分
……………6分
又由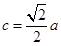 解得
解得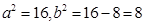 故椭圆方程为
故椭圆方程为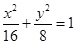 ……………8分
……………8分
(Ⅲ)由(Ⅱ)可以求得|AB|=2|OA|=2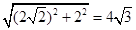 ……………9分
……………9分
假设在椭圆上存在点M使得三角形MAB的面积等于8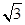
设点M到直线AB的距离为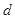 ,则应有
,则应有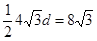
∴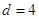 ……………10分
……………10分
与AB平行且距离为4的直线为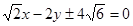
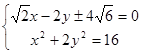 消去x得
消去x得 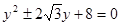
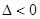 ……………13分
……………13分
此方程无解故椭圆上不存在点M使得三角形MAB的面积等于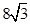 ……………14分
……………14分
另解:设点P(4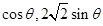 )为椭圆上任意一点
)为椭圆上任意一点
则P到直线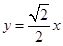 的距离为
的距离为
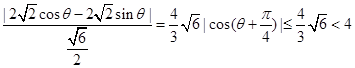 ……………13分
……………13分
故椭圆上不存在点M使得三角形MAB的面积等于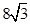 ……………14分
……………14分
(1)根据已知的向量关系,直线过原点,并且向量的垂直关系可以得到点A的坐标,然后将点A的坐标代入椭圆方程中可知得到直线的方程。
(2)连结AF1、BF1、AF2、BF2,由椭圆的对称性可知,参数a,bc的关系式,进而得到椭圆的方程。
(3)由于由(Ⅱ)可以求得|AB|=2|OA|
假设在椭圆上存在点M使得三角形MAB的面积等于8
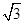
设点M到直线AB的距离为d,则应有
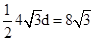
利用三角形的面积公式得到。
解:(Ⅰ)由
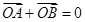 知,直线AB经过原点,又由
知,直线AB经过原点,又由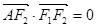 知
知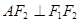 ,因为椭圆的离心率等于
,因为椭圆的离心率等于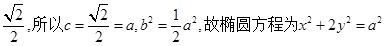 ……2分
……2分设A(
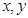 ),由
),由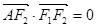 知
知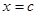
∴A(
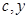 ),代入椭圆方程得
),代入椭圆方程得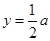 ∴A(
∴A(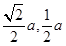 ),故直线AB的斜率
),故直线AB的斜率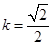
因此直线AB的方程为
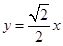 ……………4分
……………4分(Ⅱ)连结AF1、BF1、AF2、BF2,由椭圆的对称性可知
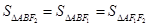 ,所以
,所以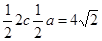 ……………6分
……………6分又由
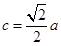 解得
解得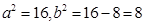 故椭圆方程为
故椭圆方程为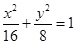 ……………8分
……………8分(Ⅲ)由(Ⅱ)可以求得|AB|=2|OA|=2
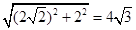 ……………9分
……………9分假设在椭圆上存在点M使得三角形MAB的面积等于8
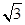
设点M到直线AB的距离为
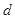 ,则应有
,则应有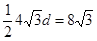
∴
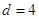 ……………10分
……………10分与AB平行且距离为4的直线为
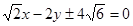
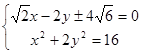 消去x得
消去x得 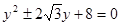
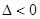 ……………13分
……………13分此方程无解故椭圆上不存在点M使得三角形MAB的面积等于
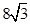 ……………14分
……………14分另解:设点P(4
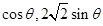 )为椭圆上任意一点
)为椭圆上任意一点则P到直线
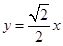 的距离为
的距离为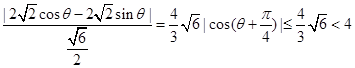 ……………13分
……………13分故椭圆上不存在点M使得三角形MAB的面积等于
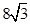 ……………14分
……………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
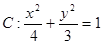 的右顶点是
的右顶点是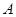 ,上下两个顶点分别为
,上下两个顶点分别为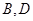 ,四边形
,四边形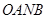 是矩形(
是矩形( 为原点),点
为原点),点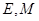 分别为线段
分别为线段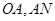 的中点.
的中点.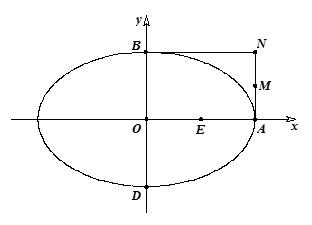
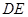 与直线
与直线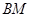 的交点在椭圆
的交点在椭圆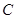 上;
上;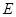 的直线交椭圆于
的直线交椭圆于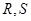 两点,
两点,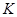 为
为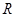 关于
关于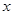 轴的对称点(
轴的对称点(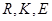 不共线),
不共线),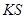 是否经过
是否经过 +
+ =1的左、右焦点,c=
=1的左、右焦点,c= ,若直线x=
,若直线x= 上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )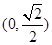



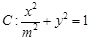 的左、右焦点分别为
的左、右焦点分别为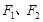 ,离心率为
,离心率为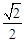 .
.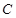 的方程;
的方程;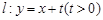 与椭圆
与椭圆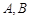 两点.若原点
两点.若原点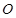 在以线段
在以线段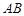 为直径的圆内,
为直径的圆内,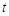 的取值范围.
的取值范围.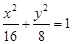 两焦点
两焦点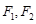 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点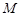 ,使得△
,使得△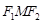 为直角三角形;
为直角三角形;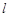 过抛物线
过抛物线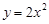 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于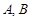 两点,则
两点,则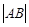 的最小值为2;
的最小值为2;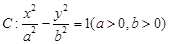 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为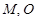 为坐标原点,则
为坐标原点,则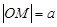 ;
; 和
和 ,又过点
,又过点 .
. 在这个椭圆上,且
在这个椭圆上,且 ,求
,求 的余弦的大小.
的余弦的大小. ,如果
,如果 的最小值为m,则满足
的最小值为m,则满足 的整点
的整点 的个数为 ( )
的个数为 ( )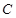 :
: 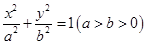 过点(0,4),离心率为
过点(0,4),离心率为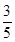 .
.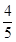 的直线被
的直线被 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 等于( )
等于( )


