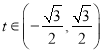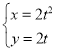题目内容
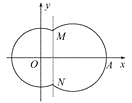
【题目】设不等式
确定的平面区域为U，
确定的平面区域为V.
（1）定义横、纵坐标为整数的点为“整点”，在区域U内任取3个整点，求这些整点中恰有2个整点在区域V内的概率；
（2）设集合
；集合
若从集合A到集合B可以建立m个不同的映射？从集合B到集合A可以建立n个不同的映射，求m，n的值.
【答案】（1）
；（2）
，
【解析】
（1）用列举法求出平面区域U的整点的个数，平面区域V的整点个数，再由古典概型概率公式求解；
（2）用列举法化简集合
，再由映射概念求解
的值.
解:（1）由题意可知平面U的整点为
，
，
，
，
，
，
，
，
，
，
，
，
，共13个；平面V的整点为，，，，，共5个；则
（2）集合
，
，要得到一个从集合
到集合
的映射，需要给集合中的5个元素在集合中都找到唯一确定的元素，共有
种不同的找法，即从集合到集合可以建立243个不同的映射，同理，从集合到集合可以建立
个不同的映射.
故；
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
