题目内容
【题目】已知函数f(x)=ex(其中e为自然对数的底数),g(x)= ![]() x+m(m,n∈R).
x+m(m,n∈R).
(1)若T(x)=f(x)g(x),m=1﹣ ![]() ,求T(x)在[0,1]上的最大值;
,求T(x)在[0,1]上的最大值;
(2)若m=﹣ ![]() ,n∈N* , 求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2<
,n∈N* , 求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2< ![]() ].
].
【答案】
(1)解:T(x)=f(x)g(x)
=ex( ![]() x+m)=ex(
x+m)=ex( ![]() x+1﹣
x+1﹣ ![]() );
);
故T′(x)=ex( ![]() x+1);
x+1);
则当n≥﹣2时,T′(x)≥0;
故T(x)在[0,1]上的最大值为T(1)=e;
当n<﹣2时,x∈[0,﹣ ![]() )时,T′(x)>0;x∈(﹣
)时,T′(x)>0;x∈(﹣ ![]() ,1]时,T′(x)<0;
,1]时,T′(x)<0;
T(x)在[0,1]上的最大值为T(﹣ ![]() )=﹣
)=﹣ ![]()
(2)解:由题意,f(x)=ex,g(x)= ![]() x﹣
x﹣ ![]() ;
;
故f(x)的图象恒在g(x)图象上方可化为
F(x)=f(x)﹣g(x)=ex﹣ ![]() x+
x+ ![]() >0恒成立;F′(x)=ex﹣
>0恒成立;F′(x)=ex﹣ ![]() ;
;
故F(x)在(﹣∞,ln ![]() )上是减函数,在(ln
)上是减函数,在(ln ![]() ,+∞)上是增函数;
,+∞)上是增函数;
故可化为F(ln ![]() )>0;即
)>0;即 ![]() (1﹣ln
(1﹣ln ![]() )+
)+ ![]() >0;
>0;
令G(n)= ![]() (1﹣ln
(1﹣ln ![]() )+
)+ ![]() ;故G′(n)=﹣
;故G′(n)=﹣ ![]() (ln
(ln ![]() +1)<0;
+1)<0;
故G(n)= ![]() (1﹣ln
(1﹣ln ![]() )+
)+ ![]() 是[1,+∞)上的减函数,
是[1,+∞)上的减函数,
而G(2e2)=﹣e2+ ![]() >0;G(14)=7(1﹣ln7)+
>0;G(14)=7(1﹣ln7)+ ![]() >0;
>0;
G(15)=7.5(1﹣ln7.5)+ ![]() <0;故最大正整数n为14
<0;故最大正整数n为14
【解析】(1)T(x)=f(x)g(x)=ex( ![]() x+m)=ex(
x+m)=ex( ![]() x+1﹣
x+1﹣ ![]() );求导T′(x)=ex(
);求导T′(x)=ex( ![]() x+1);从而确定函数的最大值;(2)由题意,f(x)=ex,g(x)=
x+1);从而确定函数的最大值;(2)由题意,f(x)=ex,g(x)= ![]() x﹣
x﹣ ![]() ;故f(x)的图象恒在g(x)图象上方可化为F(x)=f(x)﹣g(x)=ex﹣
;故f(x)的图象恒在g(x)图象上方可化为F(x)=f(x)﹣g(x)=ex﹣ ![]() x+
x+ ![]() >0恒成立;从而化为最值问题.
>0恒成立;从而化为最值问题.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 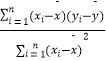 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.