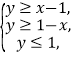��Ŀ����
����Ŀ��������{an}�����k��N*����1 �� ��2 �� ������k��R��ʹan+k=��1an+k��1+��2an+k��2+��+��kan����������n��N* �� ���{an}Ϊk�ݹ����У����������������ۣ� ����{an}�ǵȱ����У���{an}Ϊ1�ݹ����У�
����{an}�ǵȲ����У���{an}Ϊ2�ݹ����У�
��������{an}��ͨ�ʽΪ ![]() ����{an}Ϊ3�ݹ����У�
����{an}Ϊ3�ݹ����У�
���У���ȷ���۵ĸ����ǣ� ��
A.0
B.1
C.2
D.3
���𰸡�D
���������⣺�١�{an}�ǵȱ����У�
��an= ![]() ��an+1=qan��
��an+1=qan��
��k=1����=q��ʹan+k=qan+k��1������
��{an}Ϊ1�ݹ����У��ʢٳ������ڡ�{an}�ǵȲ����У�
��an=a1+��n��1��d��
��k=2����1=2����2=��1��ʹan+2=��1an+k��1+��2an+k��2������
��{an}Ϊ2�ݹ����У��ʢڳ������ۡ�������{an}��ͨ�ʽΪ ![]() ��
��
��k=3����1=3����2=��3����3=1��ʹan+3=��1an+k��1+��2an+k��2+��3an+k��3������
��{an}Ϊ3�ݹ����У��ʢ۳�����
��ѡD��
�����㾫�������ø����������ٶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���� ���ҡ��� ���ǡ�����ֵ�ж�:����p����ʽ��������������F������෴����p��q����ʽ�������P��qͬΪ��ʱΪ�棬�������ʱΪ�٣���p��q����ʽ�������p��qͬΪ��ʱΪ�٣��������ʱΪ�森