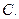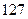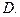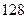题目内容
是否存在都大于2的一对实数a、b(a>b)使得ab,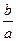 ,a–b,a+b可以按照某一次序排成一个等比数列,若存在,求出a、b的值,若不存在,说明理由.
,a–b,a+b可以按照某一次序排成一个等比数列,若存在,求出a、b的值,若不存在,说明理由.
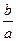 ,a–b,a+b可以按照某一次序排成一个等比数列,若存在,求出a、b的值,若不存在,说明理由.
,a–b,a+b可以按照某一次序排成一个等比数列,若存在,求出a、b的值,若不存在,说明理由.此当a=7+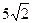 ,b=
,b=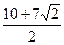 时,ab,a+b,a–b,
时,ab,a+b,a–b,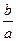 成等比数列.
成等比数列.
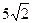 ,b=
,b=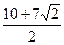 时,ab,a+b,a–b,
时,ab,a+b,a–b,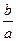 成等比数列.
成等比数列. ∵a>b,a>2,b>2,
∴ab,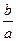 ,a–b,a+b均为正数,且有ab>a+b>
,a–b,a+b均为正数,且有ab>a+b>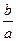 ,ab>a+b>a–b.
,ab>a+b>a–b.
假设存在一对实数a,b使ab,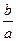 ,a+b,a–b按某一次序排成一个等比数列,则此数列必是单调数列. 不妨设该数列为单调减数列,则存在的等比数列只能有两种情形,即
,a+b,a–b按某一次序排成一个等比数列,则此数列必是单调数列. 不妨设该数列为单调减数列,则存在的等比数列只能有两种情形,即
①ab,a+b,a–b,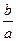 , 或 ②ab,a+b,
, 或 ②ab,a+b,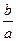 ,a–b由(a+b)2≠ab·
,a–b由(a+b)2≠ab·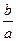
所以②不可能是等比数列,若①为等比数列,则有:
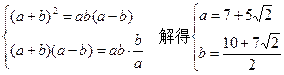
经检验知这是使ab,a+b,a–b,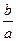 成等比数列的惟一的一组值. 因此当a=7+
成等比数列的惟一的一组值. 因此当a=7+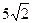 ,b=
,b=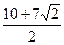 时,ab,a+b,a–b,
时,ab,a+b,a–b,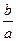 成等比数列.
成等比数列.
∴ab,
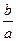 ,a–b,a+b均为正数,且有ab>a+b>
,a–b,a+b均为正数,且有ab>a+b>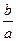 ,ab>a+b>a–b.
,ab>a+b>a–b.假设存在一对实数a,b使ab,
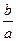 ,a+b,a–b按某一次序排成一个等比数列,则此数列必是单调数列. 不妨设该数列为单调减数列,则存在的等比数列只能有两种情形,即
,a+b,a–b按某一次序排成一个等比数列,则此数列必是单调数列. 不妨设该数列为单调减数列,则存在的等比数列只能有两种情形,即①ab,a+b,a–b,
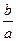 , 或 ②ab,a+b,
, 或 ②ab,a+b,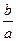 ,a–b由(a+b)2≠ab·
,a–b由(a+b)2≠ab·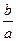
所以②不可能是等比数列,若①为等比数列,则有:
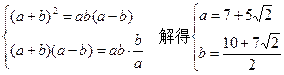
经检验知这是使ab,a+b,a–b,
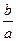 成等比数列的惟一的一组值. 因此当a=7+
成等比数列的惟一的一组值. 因此当a=7+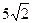 ,b=
,b=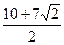 时,ab,a+b,a–b,
时,ab,a+b,a–b,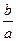 成等比数列.
成等比数列. 
练习册系列答案
相关题目
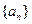 中,
中,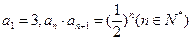 ,则
,则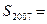 _________________
_________________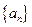 中,
中,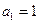 ,
,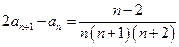 ,
, .
.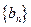 成等比数列; (2)求
成等比数列; (2)求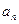 .
.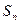 为等比数列
为等比数列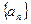 前
前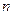 项和,
项和, ,
, ,则
,则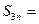 .
. 为数列
为数列 的前
的前 项和,
项和, 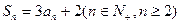 ,求数列
,求数列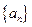 中,已知
中,已知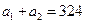 ,
,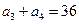 ,则
,则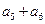 =
= 是公比为正数的等比数列,若
是公比为正数的等比数列,若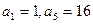 ,则数列
,则数列