题目内容
15.如图,甲、乙两个企业的用电负荷量y关于投产持续时间t(单位:小时)的关系y=f(t)均近似地满足函数f(t)=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π).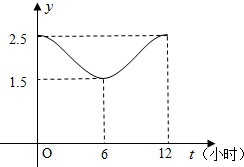
(1)根据图象,求函数f(t)的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过4.5,现采用错峰用电的方式,让企业乙比企业甲推迟m(m>0)小时投产,求m的最小值.
分析 (1)由图象可求得A,b,T的值,由周期公式可求ω,又函数图象过点(0,2.5),得sinφ=1,由范围0<φ<π,可求φ,从而可得函数f(t)的解析式;
(2)设乙投产持续时间为t小时,则甲的投产持续时间为(t+m)小时,依题意,有$f(t+m)+f(t)=\frac{1}{2}[cos\frac{π}{6}(t+m)+cos\frac{π}{6}t]+4≤\frac{9}{2}$恒成立,展开由三角函数恒等变换化简整理可得:$cos\frac{π}{6}m≤-\frac{1}{2}$,依据余弦函数图象得:$\frac{2π}{3}+2kπ≤\frac{π}{6}m≤\frac{4π}{3}+2kπ,(k∈Z)$,取k=0得m的范围,从而可求m的最小值.
解答 (本题满分14分).
解:(1)由图象可得:$\left\{{\begin{array}{l}{A+b=2.5}\\{-A+b=1.5}\end{array}}\right.$,
解得$A=\frac{1}{2},b=2$----------------------(2分)
周期T=12,∴$ω=\frac{2π}{12}=\frac{π}{6}$,---------------(3分)
∴$f(t)=\frac{1}{2}sin(\frac{π}{6}t+φ)+2$,
又∵y=f(t)过点(0,2.5),∴sinφ=1,且0<φ<π,∴$φ=\frac{π}{2}$,-----------------(5分)
∴$f(t)=\frac{1}{2}sin(\frac{π}{6}t+\frac{π}{2})+2(t≥0)$---------------(6分)
(2)设乙投产持续时间为t小时,则甲的投产持续时间为(t+m)小时
由诱导公式,企业乙用电负荷量随持续时间t变化的关系式为:$f(t)=\frac{1}{2}cos\frac{π}{6}t+2$;
同理,企业甲用电负荷量变化关系式为:$f(t+m)=\frac{1}{2}cos\frac{π}{6}(t+m)+2$;
两企业用电负荷量之和$f(t+m)+f(t)=\frac{1}{2}[cos\frac{π}{6}(t+m)+cos\frac{π}{6}t]+4(t≥0)$;------(8分)
依题意,有$f(t+m)+f(t)=\frac{1}{2}[cos\frac{π}{6}(t+m)+cos\frac{π}{6}t]+4≤\frac{9}{2}$恒成立,
即$cos\frac{π}{6}(t+m)+cos\frac{π}{6}t≤1$恒成立,
展开有:$(cos\frac{π}{6}m+1)cos\frac{π}{6}t-sin\frac{π}{6}msin\frac{π}{6}t≤1$恒成立,------(10分)
∵$(cos\frac{π}{6}m+1)cos\frac{π}{6}t-sin\frac{π}{6}msin\frac{π}{6}t=\sqrt{{{(cos\frac{π}{6}m+1)}^2}+{{sin}^2}\frac{π}{6}m}cos(\frac{π}{6}t+ϕ)$
(其$cosϕ=\frac{{cos\frac{π}{6}m+1}}{{\sqrt{{{(cos\frac{π}{6}m+1)}^2}+{{sin}^2}\frac{π}{6}m}}};sinϕ=\frac{{sin\frac{π}{6}m}}{{\sqrt{{{(cos\frac{π}{6}m+1)}^2}+{{sin}^2}\frac{π}{6}m}}}$);
∴$\sqrt{{{(cos\frac{π}{6}m+1)}^2}+{{sin}^2}\frac{π}{6}m}≤1$,-----------------------(11分)
整理得到:$cos\frac{π}{6}m≤-\frac{1}{2}$,------------------------(12分)
依据余弦函数图象得:$\frac{2π}{3}+2kπ≤\frac{π}{6}m≤\frac{4π}{3}+2kπ,(k∈Z)$,
即12k+4≤m≤12+8,取k=0得:4≤m≤8
∴m的最小值为4.-----------------------(14分)
点评 本题考查三角函数图象和性质及其应用、恒等变换等知识,考查建立三角函数模型,数据处理能力、运算求解能力和抽象概括能力,考查函数与方程的思想、转化与化归的思想,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (-2,1) | B. | (-∞,-2)∪(1,+∞) | C. | (-∞,1)∪(2,+∞) | D. | (-1,2) |
 已知某几何体的三视图如图所示,正视图和侧视图是边长为1的正方形,俯视图是腰长为1的等腰直角三角形,则该几何体的体积是( )
已知某几何体的三视图如图所示,正视图和侧视图是边长为1的正方形,俯视图是腰长为1的等腰直角三角形,则该几何体的体积是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
| A. | $\frac{2}{3}$ | B. | 2 | C. | 4 | D. | 6 |
| A. | 2° | B. | 4° | C. | 2 | D. | 4 |