题目内容
【题目】已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,坐标原点为
两点,坐标原点为![]() ,且
,且![]() 12.
12.
(Ⅰ)求抛物线的方程;
(Ⅱ)当以![]() 为直径的圆的面积为
为直径的圆的面积为![]() 时,求
时,求![]() 的面积
的面积![]() 的值.
的值.
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ)![]() 的面积为4.
的面积为4.
【解析】试题分析:(I)将![]() 代入
代入![]() ,利用韦达定理可得,
,利用韦达定理可得,![]() ,利用
,利用![]() ,可得
,可得![]() ,代入即可得到
,代入即可得到![]() 的值;(Ⅱ)根据(I)中
的值;(Ⅱ)根据(I)中![]() 的值,将
的值,将![]() 化为
化为![]() ,可得到
,可得到![]() 的式子,由直径
的式子,由直径![]() ,解方程可求出
,解方程可求出![]() 的值,进而可求出
的值,进而可求出![]() 的面积
的面积![]() 的值.
的值.
试题解析:(I)设![]() ,代入
,代入![]() ,得
,得![]()
设点![]() ,则
,则![]() ,则
,则![]() ,
,
因为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() .
.
所以抛物线的方程为![]() .
.
(Ⅱ)由(I)![]() 化为
化为![]() ,则
,则![]() .
.
又![]() ,
,
因为以![]() 为直径的圆的面积为
为直径的圆的面积为![]() ,
,
所以圆的半径为4,直径![]() .
.
则![]() ,得
,得![]() ,得
,得![]() ,得
,得![]() ,得
,得![]() (舍去)或
(舍去)或![]() ,解得
,解得![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,所以
,所以![]() 的面积为
的面积为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,所以
,所以![]() 的面积为
的面积为![]() .
.
综上,![]() 的面积为4.
的面积为4.

练习册系列答案
相关题目
【题目】大家知道, 莫言是中国首位获得诺贝尔奖的文学家, 国人欢欣鼓舞.某高校文学社从男女生中各抽取![]() 名同学调查对莫言作品的了解程度, 结果如下:
名同学调查对莫言作品的了解程度, 结果如下:
阅读过莫言的作品数( 篇) |
|
|
|
|
|
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(1)试估计该校学生阅读莫言作品超过![]() 篇的概率;
篇的概率;
(2)对莫言作品阅读超过![]() 篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过
篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过![]() 的前提下, 认为对莫言作品非常了解与性别有关?
的前提下, 认为对莫言作品非常了解与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: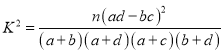 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|