题目内容
13.在△ABC中,AB=6,AC=4,$\overrightarrow{AB}•\overrightarrow{AC}=12$,则△ABC的面积为6$\sqrt{3}$.分析 由数量积的定义,求出角cosA,再求出sinA,再根据三角形的面积公式计算即可.
解答 解:设AB=b=6,BC=a,AC=c=4,
∵$\overrightarrow{AB}•\overrightarrow{AC}=12$,AB=6,AC=4,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cosA,
∴6×4cosA=12,
∴cosA=$\frac{1}{2}$,
∴sinA=$\frac{\sqrt{3}}{2}$,
∴S△ABC=$\frac{1}{2}$AB•ACsinA=$\frac{1}{2}×$6×4×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,
故答案为:6$\sqrt{3}$.
点评 本题考查平面向量的数量积的定义,三角形面积公式的应用,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.命题p:y=|sinx|是偶函数,命题q:y=sin|x|是周期为π的周期函数,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∧q | D. | (¬p)∨q |
5.已知等差数列{an},Sn是其前n项和,若a5+a11=3a10,则S27=( )
| A. | 0 | B. | 1 | C. | 27 | D. | 54 |
2.函数y=$\frac{1}{x-1}$+lnx的定义域是( )
| A. | {x|x>1} | B. | {x|0<x<1或1<x<+∞} | C. | {x|x>0} | D. | {x|x<0或x>1} |
3.某校高三年级本学期共进行了四次阶段考试,在每份数学试卷中,第Ⅰ卷共10道选择题,每小题得对的5分,答错得0分,学生甲、乙在四次考试中选择题答错的题目数如下所示:
(1)求学生甲在这四次考试中选择题答对的题目的平均数及这四次考试中第Ⅰ卷的平均得分;
(2)记以甲每次考试答错的题目数为元素构成集合A,以乙每次考试答错的题目数为元素构成集合B,在直角坐标平面上有点P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,求满足k≥2的事件的概率.
| 甲 | 3 | 2 | 0 | 1 |
| 乙 | 4 | 3 | 2 | 0 |
(2)记以甲每次考试答错的题目数为元素构成集合A,以乙每次考试答错的题目数为元素构成集合B,在直角坐标平面上有点P(x,y),Q(-1,-2),其中x∈A,y∈B,记直线PQ的斜率为k,求满足k≥2的事件的概率.
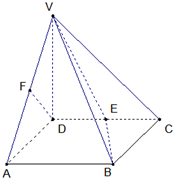 如图ABCD为正方形,VD⊥平面ABCD,VD=AD=2,F为VA中点,E为CD中点.
如图ABCD为正方形,VD⊥平面ABCD,VD=AD=2,F为VA中点,E为CD中点.