题目内容
9.解方程:sinx+cosx=cos2x,x∈R.分析 sinx+cosx=cos2x,x∈R.利用倍角公式及其因式分解可得:可得cosx+sinx=0,cosx-sinx=1,化简解出即可.
解答 解:∵sinx+cosx=cos2x,x∈R.
∴sinx+cosx=cos2x-sin2x,
∴(cosx+sinx)(cosx-sinx-1)=0,
∴cosx+sinx=0,或cosx-sinx=1,
由cosx+sinx=0,可得:tanx=-1,解得x=$-\frac{π}{4}$+kπ,(k∈Z),即解集为{x|x=$-\frac{π}{4}$+kπ,k∈Z};
cosx-sinx=1,化为$\sqrt{2}sin(x-\frac{π}{4})$=-1,∴$sin(x-\frac{π}{4})$=-$\frac{\sqrt{2}}{2}$,解得$x=\frac{π}{4}$+2kπ$-\frac{π}{4}$,或x=$\frac{π}{4}$+2kπ+$π+\frac{π}{4}$(k∈Z),
即解集为{x|x=2kπ,或x=$2kπ+\frac{3π}{2}$,k∈Z}.
综上可得:原方程的解集为{x|x=2kπ,或x=$2kπ+\frac{3π}{2}$,x=kπ-$\frac{π}{4}$,k∈Z}.
点评 本题考查了倍角公式、和差公式、三角函数的图象与性质、因式分解方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.已知a=3-2,b=0.3-2,c=log0.32,根据右边程序框图,输出的数是( )
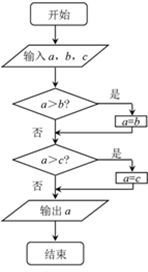

| A. | 3-2 | B. | 0.3-2 | C. | log0.32 | D. | 无法确定 |
4.若函数f(x)=x2-2x,x∈[-2,4],则f(x)的值域为( )
| A. | [-1,8] | B. | [-1,16] | C. | [-2,8] | D. | [-2,4] |
14.下列说法正确的个数是( )
①长方形绕一条直线旋转一周所形成的几何体是圆柱;
②过圆锥侧面上一点有无数条母线;
③圆锥的母线互相平行;
④夹在圆柱的两个截面间的几何体还是一个圆柱.
①长方形绕一条直线旋转一周所形成的几何体是圆柱;
②过圆锥侧面上一点有无数条母线;
③圆锥的母线互相平行;
④夹在圆柱的两个截面间的几何体还是一个圆柱.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.圆周上有10个等分点,任选3个构成三角形,其中钝角三角形的个数为( )
| A. | 30 | B. | 40 | C. | 60 | D. | 120 |