题目内容
【题目】如图，已知PA⊥平面ABCD，且四边形ABCD为矩形，M、N分别是AB、PC的中点．
（1）求证：MN⊥CD；
（2）若∠PDA＝45°，求证：MN⊥平面PCD.
【答案】见解析
【解析】证明：(1）如图所示，取PD的中点E，连接AE、NE，
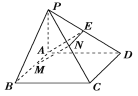
∵N为PC的中点，E为PD的中点，∴NE∥CD且NE＝
CD，而AM∥CD
且AM＝AB＝CD，∴NE∥AM且NE＝AM，∴四边形AMNE为平行四边形，
∴MN∥AE.又PA⊥平面ABCD，∴PA⊥CD，又∵ABCD为矩形，∴AD⊥CD，又AD∩PA＝A，∴CD⊥平面PAD，∴CD⊥AE，又AE∥MN，∴MN⊥CD.
(2）由(1）可知CD⊥AE，MN∥AE.又∠PDA＝45°，∴△PAD为等腰直角三角形，
又E为PD的中点，∴AE⊥PD，∴AE⊥平面PCD. 又AE∥MN，∴MN⊥平面PCD.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
