题目内容
3.已知集合A={x|x2-x<0},B={x|x2+2mx+2m+1<0},A∪B=A,求实数m的取值范围.分析 求出A中不等式的解集确定出A,根据A与B的并集为A,分B为空集及不为空集两种情况,分别列出关于m的不等式,求出不等式的解集即可确定出m的范围.
解答 解:由题设A=(0,1),
∵A∪B=A,
∴B⊆A,
B=∅,△=4m2-4(2m+1)≤0,∴1-$\sqrt{2}$≤m≤1+$\sqrt{2}$.
B≠∅,m<1-$\sqrt{2}$或m>1+$\sqrt{2}$,且$\left\{\begin{array}{l}{0<-m<1}\\{2m+1<0}\\{1+2m+2m+1<0}\end{array}\right.$,∴-1<m<1-$\sqrt{2}$.
综上,-1<m≤1+$\sqrt{2}$.
点评 此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
13.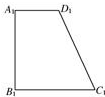 如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
 如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{2}$ | C. | 24$\sqrt{2}$ | D. | 24 |
12.已知P=log45,Q=log54,R=log4(log54),则( )
| A. | R<Q<P | B. | P<R<Q | C. | Q<R<P | D. | R<P<Q |
 已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.
已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.