题目内容
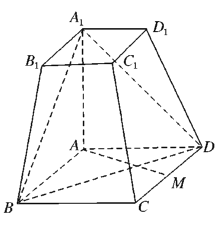
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() ,四边形
,四边形![]() 满足
满足![]() ,
,![]() 为侧棱
为侧棱![]() 上的任意一点.
上的任意一点.

(1)求证:平面![]() 平面
平面![]() .
.
(2)是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 垂直?若存在,写出证明过程并求出线段
垂直?若存在,写出证明过程并求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)证明见解析(2)存在点![]() ,证明见解析;线段
,证明见解析;线段![]() 的长为
的长为![]()
【解析】
(1)由平面![]() 平面
平面![]() ,易得
,易得![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,根据线面垂直的判定定理,得
,根据线面垂直的判定定理,得![]() 平面
平面![]() ,再由面面垂直的判定定理,得平面
,再由面面垂直的判定定理,得平面![]() 平面
平面![]() .
.
(2)这是一个探索性问题,将问题倒推来分析,若有直线![]() 与平面
与平面![]() 垂直,根据点F,即证使
垂直,根据点F,即证使![]() 的位置.
的位置.
(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
且![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() .
.
又![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)存在点![]() ,当
,当![]() 时,直线
时,直线![]() 与平面
与平面![]() 垂直.
垂直.
证明如下:
由![]() ,
,
得![]() ,
,
![]() .
.
又![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() .
.
又![]() ,
,
![]() 平面
平面![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
∴存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 垂直.此时线段
垂直.此时线段![]() 的长为
的长为![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目