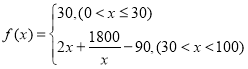题目内容
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)若![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得 ,
, 都成立?请说明理由.
都成立?请说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析.
;(2)不存在,理由见解析.
【解析】
(1)根据![]() 的奇偶性和单调性,将函数值的比较变为自变量的比较,得到
的奇偶性和单调性,将函数值的比较变为自变量的比较,得到![]() 恒成立,利用参变分离,得到
恒成立,利用参变分离,得到![]() 的取值范围;(2)假设
的取值范围;(2)假设![]() 存在,整理
存在,整理 和
和 ,设
,设![]() ,
,![]() ,
,![]()
得到![]() ,按照
,按照![]() 和
和![]() 进行分类讨论,从而证明不存在所需的
进行分类讨论,从而证明不存在所需的![]() .
.
(1)![]() ,为
,为![]() 上的奇函数,单调递减,
上的奇函数,单调递减,
所以![]() 恒成立,
恒成立,
可得![]()
所以![]() 恒成立
恒成立
即![]() 恒成立,
恒成立,
当![]() 时,该不等式恒成立,
时,该不等式恒成立,
当![]() 时,
时,![]() ,
,
设![]() ,则
,则
![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
所以![]() .
.
(2)![]()
所以 ,
,

假设存在实数![]() ,使得
,使得![]() 和
和![]() 都成立,
都成立,
设![]() ,
,![]() ,
,![]()
则![]() ,
,
![]() ,
,
若![]() ,则
,则![]() ,解得
,解得![]() ,
,![]() 或
或![]() ,
,![]() ,均不是有理数,
,均不是有理数,
若![]() ,则
,则![]() ,其中
,其中![]() ,而
,而![]() ,所以不成立,
,所以不成立,
综上所述,故不存在实数![]() ,使得
,使得 ,
, 都成立.
都成立.

 阅读快车系列答案
阅读快车系列答案【题目】已知△ABC的边AB所在直线方程为y=3x,BC所在直线方程为y=ax+12,AC边上的高BD所在直线方程为y=﹣x+8.
(1)求实数a的值;
(2)若AC边上的高BD![]() ,求边AC所在的直线方程.
,求边AC所在的直线方程.
【题目】某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率有帮助”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
60分及以下 | 61~70分 | 71~80分 | 81~90分 | 91~100分 | |
甲班(人数) | 3 | 6 | 12 | 15 | 9 |
乙班(人数) | 4 | 7 | 16 | 12 | 6 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)由以上统计数据填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
(2)对甲乙两班60分及以下的同学进行定期辅导,一个月后从中抽取3人课堂检测,![]() 表示抽取到的甲班学生人数,求
表示抽取到的甲班学生人数,求![]() 及至少抽到甲班1名同学的概率.
及至少抽到甲班1名同学的概率.