题目内容
(本小题满分14分)已知四棱锥P—ABCD的三视图如右图所示,
其中正(主)视图与侧(左)视为直角三角形,俯视图为正方形。
 (1)求四棱锥P—ABCD的体积;
(1)求四棱锥P—ABCD的体积;
 (2)若E是侧棱
(2)若E是侧棱 上的动点。问:不论点E在PA的
上的动点。问:不论点E在PA的
任何位置上,是否都有 ?
?
请证明你的结论?
(3)求二面角D—PA—B的余弦值。
其中正(主)视图与侧(左)视为直角三角形,俯视图为正方形。
 (1)求四棱锥P—ABCD的体积;
(1)求四棱锥P—ABCD的体积; (2)若E是侧棱
(2)若E是侧棱 上的动点。问:不论点E在PA的
上的动点。问:不论点E在PA的任何位置上,是否都有
 ?
?请证明你的结论?
(3)求二面角D—PA—B的余弦值。

不论点E在何位置,都有
 ,
,
解:(1)由三视图可知,四棱锥P—ABCD的底面是边长为1的正方形,
侧棱 底面ABCD,且PC=2
底面ABCD,且PC=2
 4分
4分
(2)不论点E在何位置,都有 5分
5分
证明:连结AC,
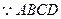 是正方形,
是正方形,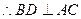
 底面ABCD,且
底面ABCD,且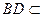 平面ABCD,
平面ABCD,
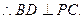 6分
6分
又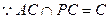 ,
,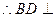 平面PAC 7分
平面PAC 7分
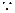 不论点E在何位置,都有
不论点E在何位置,都有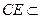 平面PAC。
平面PAC。
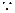 不论点E在何位置,都有BD
不论点E在何位置,都有BD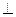 CE。 9分
CE。 9分
(3)在平面DAP过点D作DF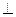 PA于F,连结BF
PA于F,连结BF
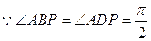 ,AD=AB=1,
,AD=AB=1,
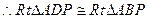
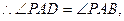
又AF=AF,AB=AD
从而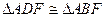 ,
,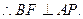
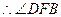 为二面角D—AP—B的平面角 12分
为二面角D—AP—B的平面角 12分
在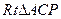 中,
中,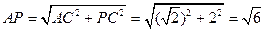
故在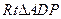 中,
中,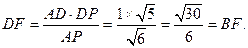
又 ,在
,在 中,
中,
由余弦定理得:
所以二面角D—PA—B的余弦值为 14分
14分
侧棱
 底面ABCD,且PC=2
底面ABCD,且PC=2 4分
4分(2)不论点E在何位置,都有
 5分
5分证明:连结AC,
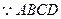 是正方形,
是正方形,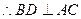
 底面ABCD,且
底面ABCD,且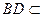 平面ABCD,
平面ABCD,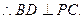 6分
6分又
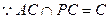 ,
,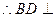 平面PAC 7分
平面PAC 7分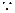 不论点E在何位置,都有
不论点E在何位置,都有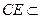 平面PAC。
平面PAC。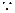 不论点E在何位置,都有BD
不论点E在何位置,都有BD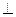 CE。 9分
CE。 9分(3)在平面DAP过点D作DF
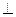 PA于F,连结BF
PA于F,连结BF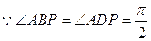 ,AD=AB=1,
,AD=AB=1,
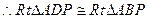
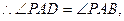
又AF=AF,AB=AD
从而
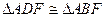 ,
,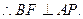
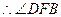 为二面角D—AP—B的平面角 12分
为二面角D—AP—B的平面角 12分在
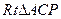 中,
中,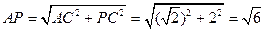
故在
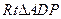 中,
中,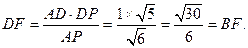
又
 ,在
,在 中,
中,由余弦定理得:

所以二面角D—PA—B的余弦值为
 14分
14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
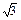
 ,2
,2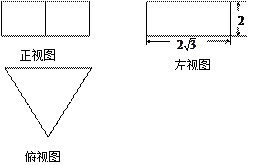
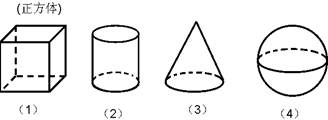
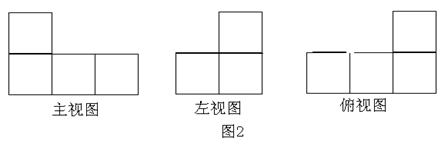

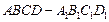 中,
中,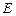 ,
,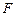 分别为
分别为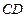 和
和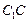 的中点,则直线
的中点,则直线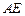 与
与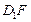 所成角的余弦值为
所成角的余弦值为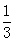
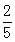

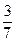
 的纬线上,且两地的经度差为
的纬线上,且两地的经度差为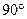 ,若地球的半径为
,若地球的半径为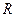 千米,且时速为20千米的轮船从A地到B地最少需要
千米,且时速为20千米的轮船从A地到B地最少需要 小时,则
小时,则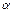 为
为 
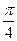
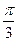
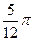
 BC,AB =" BC" = kPA,点E、D分别是AC、PC的中点,EP⊥底面ABC.
BC,AB =" BC" = kPA,点E、D分别是AC、PC的中点,EP⊥底面ABC.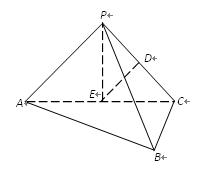
 直线AB与平面PAC所成的角;
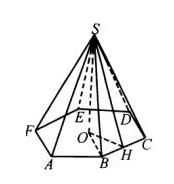
直线AB与平面PAC所成的角; 内有一个正六边形ABCDEF,它的中心是O,边长是2cm.OS⊥
内有一个正六边形ABCDEF,它的中心是O,边长是2cm.OS⊥ 点和边的距离.
点和边的距离.