题目内容
6.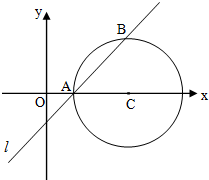 如图所示,圆C的圆心C在x轴的正半轴上,且过直线l:y=x-1与x轴的交点A,若直线l被圆C截得的弦AB的长为2$\sqrt{2}$,则圆C的标准方程为(x-3)2+y2=4.
如图所示,圆C的圆心C在x轴的正半轴上,且过直线l:y=x-1与x轴的交点A,若直线l被圆C截得的弦AB的长为2$\sqrt{2}$,则圆C的标准方程为(x-3)2+y2=4.
分析 设圆的标准方程为(x-a)2+y2=r2,由题意可得$\left\{\begin{array}{l}{|1-a|=r}\\{(\frac{|a-1|}{\sqrt{2}})^{2}+2={r}^{2}}\end{array}\right.$,求得a、r的值,可得圆的标准方程
解答 解:设圆的标准方程为(x-a)2+y2=r2,由题意可得$\left\{\begin{array}{l}{|1-a|=r}\\{(\frac{|a-1|}{\sqrt{2}})^{2}+2={r}^{2}}\end{array}\right.$,
解得:a=3,r=2,可得圆的标准方程为(x-3)2+y2=4.
故答案为:(x-3)2+y2=4.
点评 本题主要考查用点斜式求直线的方程,直线和圆相交的性质,点到直线的距离公式,属于基础题

练习册系列答案
相关题目
17.已知数列{an}的前n项和为Sn,a1=$\frac{4}{3}$,且满足3Sn+Sn-1=4(n≥2,n∈N*),若a≤-Sn+$\frac{1}{{S}_{n}}$≤b(n∈N*)恒成立,则b-a的最小值为( )
| A. | $\frac{59}{72}$ | B. | $\frac{7}{12}$ | C. | $\frac{17}{72}$ | D. | 1 |
1.已知数列{an}是递增数列,且满足an=2n2+λn,则实数λ的取值范围是( )
| A. | (0,+∞) | B. | (-4,+∞) | C. | [-4,+∞) | D. | (-6,+∞) |
18.全集U=R,A={x|x2>4},B={x|x<0},则A∩B=( )
| A. | {x|x<-2} | B. | {x|2<x<3} | C. | {x|x>3} | D. | {x|x<-2或2<x<3} |
15.若sinα=$\frac{1}{5}$,且α是第二象限角,则$\frac{sin2α+si{n}^{2}α}{co{s}^{2}α}$ 的值为( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | -$\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{6}}{6}$+$\frac{1}{24}$ | D. | -$\frac{\sqrt{6}}{6}+\frac{′1}{24}$ |
16.y=x-ex的极大值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 不存在 |