题目内容
【题目】已知函数f（x）= 
﹣ax+b，在点M（1，f（1））处的切线方程为9x+3y﹣10=0，求
（1）实数a，b的值；
（2）函数f（x）的单调区间以及在区间[0，3]上的最值．
【答案】
（1）解：因为在点M（1，f（1））处的切线方程为9x+3y﹣10=0，
所以切线斜率是k=﹣3
且9×1+3f（1）﹣10=0，
求得 
，即点 
又函数 
，则f′（x）=x2﹣a
所以依题意得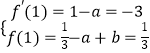 
解得 
（2）解：由（1）知 
所以f′（x）=x2﹣4=（x+2）（x﹣2）
令f′（x）=0，解得x=2或x=﹣2
当f′（x）＞0x＞2或x＜﹣2；当f′（x）＜0﹣2＜x＜2
所以函数f（x）的单调递增区间是（﹣∞，2），（2，+∞）
单调递减区间是（﹣2，2）
又x∈[0，3]
所以当x变化时，f（x）和f′（x）变化情况如下表：
X | 0 | （0，2） | 2 | （2，3） | 3 |
f′（x） | ﹣ | 0 | + | 0 | |
f（x） | 4 | ↘ | 极小值 | ↗ | 1 |
所以当x∈[0，3]时，f（x）max=f（0）=4，
【解析】（1）求出曲线的斜率，切点坐标，求出函数的导数，利用导函数值域斜率的关系，即可求出a，b．（2）求出导函数的符号，判断函数的单调性以及求解闭区间的函数的最值．
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
【题目】某产品的三个质量指标分别为x，y，z，用综合指标S=x+y+z评价该产品的等级．若S≤4，则该产品为一等品．现从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如下：
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 | （1，1，2） | （2，1，1） | （2，2，2） | （1，1，1） | （1，2，1） |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 | （1，2，2） | （2，1，1） | （2，2，1） | （1，1，1） | （2，1，2） |
（1）利用上表提供的样本数据估计该批产品的一等品率．
（2）在该样品的一等品中，随机抽取2件产品， ①用产品编号列出所有可能的结果；
②设事件B为“在取出的2件产品中，每件产品的综合指标S都等于4”，求事件B发生的概率．
