Question

【题目】圆O1和圆O2的极坐标方程分别为ρ＝4cosθ，ρ＝－4sinθ
（1）把圆O1和圆O2的极坐标方程化为直角坐标方程；
（2）求经过圆O1、圆O2交点的直线的直角坐标方程

Answer 1

【答案】
（1）

【解答】以极点为原点、极轴为x轴正半轴建立平面直角坐标系，两坐标系中取相同的长度单位．

x＝ρcosθ，y＝ρsinθ，由ρ＝4cosθ得ρ2＝4ρcosθ，

所以x2＋y2＝4x、即圆O1的直角坐标方程为x2＋y2－4x＝0，

同理圆O2的直角坐标方程为x2＋y2＋4y＝0

（2）

解：以极点为原点、极轴为x轴正半轴建立平面直角坐标系，两坐标系中取相同的长度单位．

由 解得 或者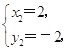

即圆O1、圆O2交于点(0，0)和(2，－2)，故过交点的直线的直角坐标方程为y＝－x

【解析】本题主要考查了圆的极坐标方程，解决问题的关键是将所给极坐标方程转化为普通方程分析计算即可
【考点精析】本题主要考查了圆的参数方程的相关知识点，需要掌握圆的参数方程可表示为才能正确解答此题．