题目内容
18. 如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.
如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.(1)求证:BC1⊥平面AC B1;
(2)求二面角B-AB1-C的大小.
分析 (1)通过证明C1B⊥B1C,AC⊥C1B,利用直线与平面垂直的判定定理证明C1B⊥平面AB1C.
(2)过B作BG⊥AB1,G为垂足,连接GO,说明∠BGO为所求二面角的平面角.设AC=2,通过解三角形求解二面角的大小;
另解:设D为AB中点,连接CD,过点D作DE⊥AB1,E为垂足,连接CE,说明∠DEC即为二面角B-AB1-C的平面角.设AC=2,通过解三角形以及三角形相似,求解二面角B-AB1-C的大小.
解答 (1)证明:由题设知B B1C1C 为正方形,所以C1B⊥B1C,
又AC⊥平面C1B,∴AC⊥C1B,∵B1C∩AC=C
∴C1B⊥平面AB1C,…(6分)
(2)解:由(1)知点O为点B在平面AB1C的射影
过B作BG⊥AB1,G为垂足,连接GO,则∠BGO
即为所求二面角的平面角.设AC=2
在Rt△AB1B中,B1B=2,AB=2$\sqrt{2}$,AB1=2$\sqrt{3}$
∴BG=$\frac{2×2\sqrt{2}}{2\sqrt{3}}$=$\frac{2\sqrt{6}}{3}$,由(1)知BO=$\sqrt{2}$,
∴在Rt△BGO中,sin∠BGO=$\frac{BO}{BG}$=$\frac{\sqrt{2}}{\frac{2\sqrt{6}}{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠BGO=60°…(12分)
另解:设D为AB中点,连接CD,则CD⊥AB,∴CD⊥平面A1B1BA,
∴点D是点C在平面A1B1BA的射影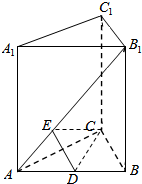 .
.
过点D作DE⊥AB1,E为垂足,连接CE,则∠DEC即为二面角B-AB1-C的平面角.
设AC=2,则CD=AD=$\sqrt{2}$,∴AB1=2$\sqrt{3}$,
∵Rt△ADE∽Rt△AB1B,∴$\frac{DE}{AD}$=$\frac{{B}_{1}B}{{AB}_{1}}$,
∴BE=$\sqrt{2}×\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,
∴tan$∠DEC=\frac{DC}{DE}$=$\frac{\sqrt{2}}{\frac{2\sqrt{6}}{3}}$=$\sqrt{3}$,∴∴∠BGO=60°.
∴二面角B-AB1-C的大小为60°.…(12分)
点评 本题考查二面角的平面角的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及逻辑推理能力.

| A. | (π,0) | B. | ($\frac{5π}{16}$,0) | C. | ($\frac{5π}{8}$,0) | D. | ($\frac{7π}{8}$,0) |
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| A. | (-∞,-1)∪(3,+∞) | B. | (-1,3) | C. | (1,3) | D. | (-∞,1)∪(3,+∞) |