题目内容
9.已知数列{an}的前n项和为Sn,an与Sn满足关系式Sn=3-$\frac{n+3}{n+1}$an(n∈N*).(Ⅰ)求a1,a2,a3,a4的值;
(Ⅱ)猜想数列{an}的通项公式,并用数学归纳法证明.
分析 (Ⅰ)利用Sn=3-$\frac{n+3}{n+1}$an(n∈N*).代入计算,可得结论;
(Ⅱ)猜想an=$\frac{n+1}{{2}^{n}}$,(n∈N*).然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:(Ⅰ)∵Sn=3-$\frac{n+3}{n+1}$an(n∈N*).
∴a1=s1=3-$\frac{1+3}{1+1}$a1,解得a1=$\frac{2}{2}$=1,
a1+a2=s2=3-$\frac{2+3}{2+1}$a2,解得a2=$\frac{3}{4}$,
a1+a2+a3=s3=3-$\frac{3+3}{3+1}$a3,解得a3=$\frac{1}{2}$=$\frac{4}{8}$,
a1+a2+a3+a4=s4=3-$\frac{4+3}{4+1}$a4,解得a4=$\frac{5}{16}$,
(Ⅱ)由(Ⅰ)可猜想an=$\frac{n+1}{{2}^{n}}$,(n∈N*).
证明:①当n=1时,a1=1,等式成立;
②假设n=k时,结论成立,即ak=$\frac{k+1}{{2}^{k}}$,(k≥2,k∈N*).
则n=k+1时,ak+1=sk+1-sk=3-$\frac{k+4}{k+2}$kk+1-3+$\frac{k+3}{k+1}$ak,
∴(1+$\frac{k+4}{k+2}$)ak+1=$\frac{k+3}{k+1}$•$\frac{k+1}{{2}^{k}}$,
∴$\frac{2(k+3)}{k+2}$ak+1=$\frac{k+3}{{2}^{k}}$,
∴ak+1=$\frac{k+1+1}{{2}^{k+1}}$,
所以当n=k+1等式成立
根据①②可知猜想成立.
点评 此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证,这是数列的通项一种常用求解的方法

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | -1 | B. | 4 | C. | -1或4 | D. | 1或5 |
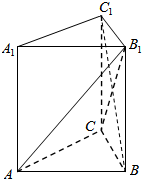 如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.
如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.