题目内容
3.已知a>0,b>0,且a+b=1,求证:$\sqrt{a+\frac{1}{2}}$+$\sqrt{b+\frac{1}{2}}$≤2.分析 运用分析法证明,注意运用平方法和基本不等式,即可得证.
解答 证明:要证 $\sqrt{a+\frac{1}{2}}$+$\sqrt{b+\frac{1}{2}}$≤2,只要证($\sqrt{a+\frac{1}{2}}$+$\sqrt{b+\frac{1}{2}}$)2≤4,
即证a+b+1+2$\sqrt{a+\frac{1}{2}}$•$\sqrt{b+\frac{1}{2}}$≤4.
只要证$\sqrt{a+\frac{1}{2}}$•$\sqrt{b+\frac{1}{2}}$≤1.
也就是要证:ab+$\frac{1}{2}$(a+b)+$\frac{1}{4}$≤1,
即证ab≤$\frac{1}{4}$.
∵a>0,b>0,a+b=1.
∴1=a+b≥2,∴ab≤$\frac{1}{4}$,即上式成立.
故$\sqrt{a+\frac{1}{2}}$+$\sqrt{b+\frac{1}{2}}$≤2.
点评 本题考查不等式的证明,主要考查分析法证明不等式的方法,注意平方法的运用,属于中档题.

练习册系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.
如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=90°,且AC=AA1.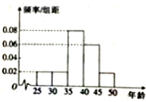 2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )
2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )