题目内容
.(本题满分15分)
已知四点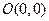 ,
,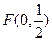 ,
,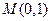 ,
,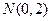 。点
。点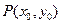 在抛物线
在抛物线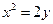 上
上
(Ⅰ) 当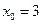 时,延长
时,延长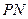 交抛物线于另一点
交抛物线于另一点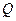 ,求
,求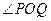 的大小;
的大小;
(Ⅱ)当点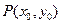
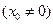 在抛物线
在抛物线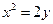 上运动时,
上运动时,
ⅰ)以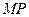 为直径作圆,求该圆截直线
为直径作圆,求该圆截直线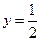 所得的弦长;
所得的弦长;
ⅱ)过点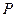 作
作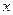 轴的垂线交
轴的垂线交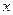 轴于点
轴于点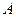 ,过点
,过点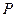 作该抛物线的切线
作该抛物线的切线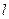 交
交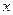 轴于点
轴于点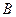 。问:是否总有
。问:是否总有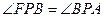 ?如果有,请给予证明;如果没有,请举出反例。
?如果有,请给予证明;如果没有,请举出反例。
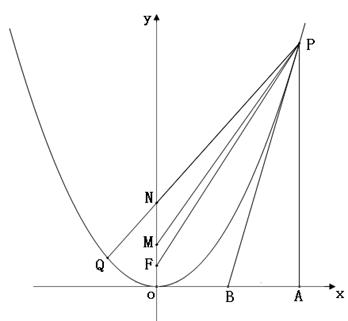
已知四点
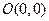 ,
,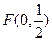 ,
,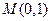 ,
,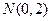 。点
。点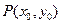 在抛物线
在抛物线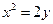 上
上(Ⅰ) 当
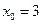 时,延长
时,延长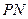 交抛物线于另一点
交抛物线于另一点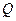 ,求
,求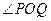 的大小;
的大小;(Ⅱ)当点
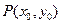
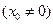 在抛物线
在抛物线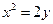 上运动时,
上运动时,ⅰ)以
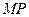 为直径作圆,求该圆截直线
为直径作圆,求该圆截直线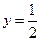 所得的弦长;
所得的弦长;ⅱ)过点
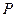 作
作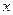 轴的垂线交
轴的垂线交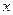 轴于点
轴于点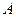 ,过点
,过点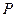 作该抛物线的切线
作该抛物线的切线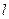 交
交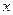 轴于点
轴于点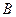 。问:是否总有
。问:是否总有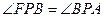 ?如果有,请给予证明;如果没有,请举出反例。
?如果有,请给予证明;如果没有,请举出反例。
(Ⅰ) 当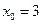 时,
时,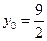 ,
,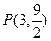 ,
,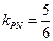
直线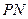 :
: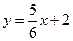 代入
代入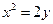 ,得
,得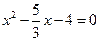 ,
,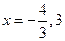 ,
,
所以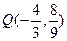 ,
,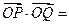
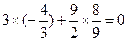 ,
,
所以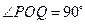 ……………5分
……………5分
(Ⅱ) ⅰ)以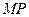 为直
为直 径的圆的圆心为
径的圆的圆心为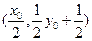 ,
,
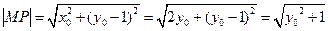 ,
,
所以圆的半径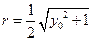 ,
,
圆心到直线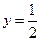 的距离
的距离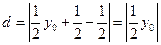 ;
;
故截得的弦长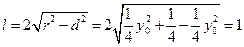 ……………1
……………1 0分
0分
(Ⅱ)总有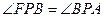 。……………11分
。……………11分
证明: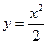 ,
,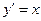 ,
,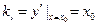 ,
,
所以切线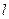 的方程为
的方程为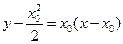 ,即
,即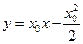
令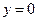 ,得
,得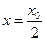 ,所以点
,所以点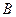 的坐标为
的坐标为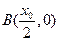 ………………12分
………………12分
点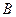 到直线
到直线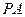 的距离
的距离 为
为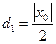 ,
,
下面求直线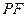 的方程
的方程
因为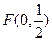 ,所以直线
,所以直线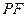 的方程为
的方程为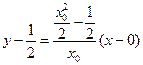 ,
,
整理得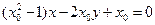
所以点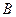 到直线
到直线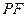 的距离为
的距离为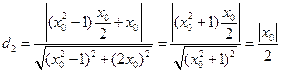 ,
,
所以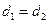
所以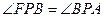 ………………15分
………………15分
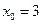 时,
时,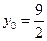 ,
,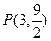 ,
,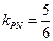
直线
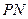 :
: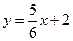 代入
代入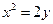 ,得
,得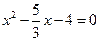 ,
,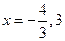 ,
,所以
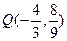 ,
,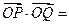
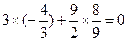 ,
,所以
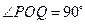 ……………5分
……………5分(Ⅱ) ⅰ)以
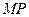 为直
为直 径的圆的圆心为
径的圆的圆心为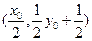 ,
,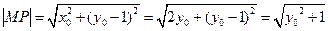 ,
,所以圆的半径
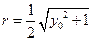 ,
,圆心到直线
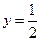 的距离
的距离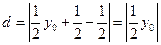 ;
;故截得的弦长
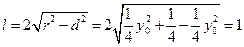 ……………1
……………1 0分
0分(Ⅱ)总有
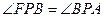 。……………11分
。……………11分证明:
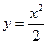 ,
,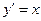 ,
,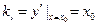 ,
,所以切线
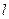 的方程为
的方程为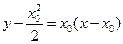 ,即
,即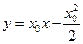
令
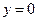 ,得
,得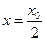 ,所以点
,所以点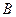 的坐标为
的坐标为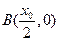 ………………12分
………………12分点
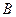 到直线
到直线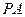 的距离
的距离 为
为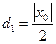 ,
,下面求直线
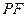 的方程
的方程因为
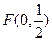 ,所以直线
,所以直线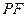 的方程为
的方程为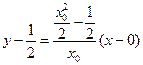 ,
,整理得
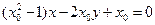
所以点
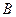 到直线
到直线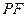 的距离为
的距离为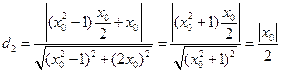 ,
,所以
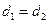
所以
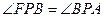 ………………15分
………………15分略

练习册系列答案
相关题目
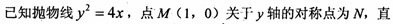

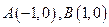 ,过曲线
,过曲线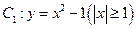 上 一点
上 一点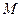 的切线
的切线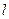 ,与曲线
,与曲线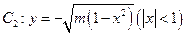 也相切于点
也相切于点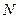 ,记点
,记点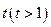 。
。
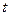 表示
表示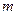 的值和点
的值和点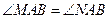 ?
?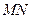 所在直线的方程。
所在直线的方程。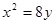
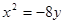
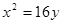
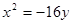
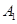 、
、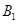 ,则∠
,则∠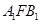 =( )
=( )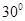 B.
B. 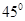 C.
C. 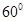 D.
D. 
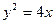 上的一点P到直线
上的一点P到直线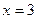 的距离与点P到点(3,0)的距离之和为4,则P点的横坐标可以为 ( )
的距离与点P到点(3,0)的距离之和为4,则P点的横坐标可以为 ( ) .3 D.4
.3 D.4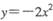 的焦点坐标是
的焦点坐标是
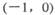

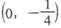
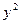 =2px(p>0)的焦点F的直线
=2px(p>0)的焦点F的直线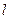 与抛物线在第一象限的交点为A,与抛物线准线的交点为B,点A在抛物线准线上的射影为C,若
与抛物线在第一象限的交点为A,与抛物线准线的交点为B,点A在抛物线准线上的射影为C,若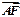 =
=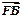 ,
,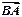 ·
·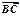 =48,则p的值为______▲_____
=48,则p的值为______▲_____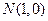 ,动点
,动点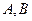
 分别在抛物线
分别在抛物线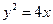 及曲线
及曲线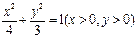 上,若
上,若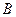 在
在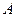 的右侧,且
的右侧,且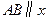 轴,则
轴,则
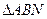 的周长
的周长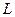 的取值范围是
的取值范围是