题目内容
已知函数
 .
.
(1)求函数 的单调区间和极值;
的单调区间和极值;
(2)若 对
对 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(1)e;(2)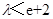
解析试题分析:(1)先求导函数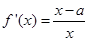 ,然后利用导数求极值的方法和对a进行分类讨论解决问题;(2)对a分
,然后利用导数求极值的方法和对a进行分类讨论解决问题;(2)对a分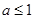 和
和 利用导数分析单调性进行分类讨论即可.
利用导数分析单调性进行分类讨论即可.
试题解析:(1)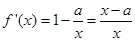
 ,
,
当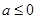 时,
时,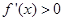 ,在
,在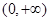 上增,无极值;
上增,无极值;
当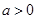 时,
时,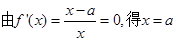 ,
, 在
在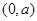 上减,在
上减,在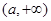 上增,
上增, 有极小值
有极小值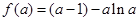 ,无极大值; 6分
,无极大值; 6分
(2)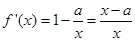 ,
,
当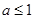 时,
时,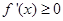 在
在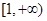 上恒成立,则
上恒成立,则 是单调递增的,
是单调递增的,
则只需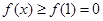 恒成立,所以
恒成立,所以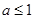 ,
,
当 时,
时, 在上
在上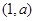 减,在
减,在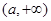 上单调递增,所以当
上单调递增,所以当 时,
时,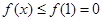 这与
这与 恒成立矛盾,故不成立,综上:
恒成立矛盾,故不成立,综上: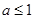 . 13分
. 13分
考点:(1)导数在函数中的应用;(2)恒成立问题.

练习册系列答案
相关题目
 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意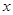 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。 是否具有“
是否具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 上有最大值;
上有最大值; 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若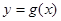 与
与 交点个数为2013,求
交点个数为2013,求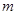 的值.
的值. ,
, .
. 的值;
的值; 的值域.
的值域.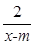 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围. .
. 时,求
时,求 的单调区间;
的单调区间; 有解,求实数m的取值菹围;
有解,求实数m的取值菹围; .
.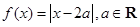 .
.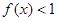 的解集为
的解集为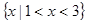 ,求
,求 的值;
的值;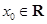 ,使
,使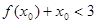 ,求
,求 。
。 的解集;
的解集; 对
对 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
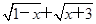 ;
; ;
;