题目内容
设命题p:f(x)=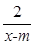 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若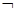 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围.
(1,+∞)
解析试题分析:先根据分式函数的单调性求出命题p为真时m的取值范围,然后根据题意求出|x1-x2|的最大值,再解不等式,若-p∧q为真则命题p假q真,从而可求出m的取值范围.
试题解析:由于f(x)=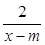 的单调递减区间是(-∞,m)和(m,+∞),而f(x)又在(1,+∞)上是减函数,所以m≤1,即p:m≤1.对于命题q:|x1-x2|=
的单调递减区间是(-∞,m)和(m,+∞),而f(x)又在(1,+∞)上是减函数,所以m≤1,即p:m≤1.对于命题q:|x1-x2|=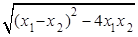 =
=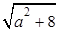 ≤3,则m2+5m-3≥3,即m2+5m-6≥0,
≤3,则m2+5m-3≥3,即m2+5m-6≥0,
解得m≥1或m≤-6,若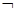 p∧q为真,则p假q真,所以
p∧q为真,则p假q真,所以 解之得m>1,因此实数m的取值范围是(1,+∞).
解之得m>1,因此实数m的取值范围是(1,+∞).
考点:1.函数恒成立问题;2.复合命题的真假.

练习册系列答案
相关题目
 .
. ),f(
),f( )是否成等比数列,并证明f(
)是否成等比数列,并证明f( 为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围. ,
,
 ,函数
,函数 的图像与直线
的图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
. 的值;
的值;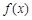 在
在 上的单调递增区间.
上的单调递增区间. 的定义域为E,值域为F.
的定义域为E,值域为F. 与集合F的关系;
与集合F的关系; },求实数a的值.
},求实数a的值. ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值. 在点
在点 处的切线方程为
处的切线方程为
 .
. 、
、 的值;
的值;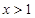 时,
时, 恒成立,求实数
恒成立,求实数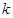 的取值范围;
的取值范围; ,且
,且 时,
时, .
. ,若函数
,若函数 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数 的取值范围.
的取值范围.
 .
. 的单调区间和极值;
的单调区间和极值; 对
对 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有 ,且当
,且当 时,
时, 。
。 是否满足这些条件;
是否满足这些条件; ,求方程
,求方程 的解。
的解。 (k∈R,且k>0).
(k∈R,且k>0).