题目内容
【题目】已知![]() 中,角
中,角![]() 所对的边分别是
所对的边分别是![]() ,
,![]() ,且
,且![]() .
.
(1)求角![]() ;
;
(2)![]() ,
,![]() 为
为![]() 所在平面内一点,且满足
所在平面内一点,且满足![]() ,求
,求![]() 的最小值,并求
的最小值,并求![]() 取得最小值时
取得最小值时![]() 的面积
的面积![]() .
.
【答案】(1)![]() .(2)
.(2)![]() 的最小值为
的最小值为![]() ,
,![]() 的面积
的面积![]() 为
为![]() .
.
【解析】
(1)由![]() ,变形可得
,变形可得![]() ,余弦定理可得
,余弦定理可得![]() ,由正弦定理得:
,由正弦定理得:![]() ,进一步化简可得
,进一步化简可得![]() ,又由
,又由![]() ,利用同角三角函数关系化简
,利用同角三角函数关系化简![]() ,
,![]() ,可求出角A;
,可求出角A;
(2)由(1)可知![]() 为直角三角形,又可得出
为直角三角形,又可得出![]() 点在以
点在以![]() 为直径的圆上,设
为直径的圆上,设![]() 为
为![]() 中点,连结
中点,连结![]() ,则当点
,则当点![]() 在
在![]() 上时,
上时,![]() 取得最小值,设
取得最小值,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,即可得出
,即可得出![]() 的面积
的面积![]() .
.
(1)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
由正弦定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 为三角形内角,
为三角形内角,![]() .
.
又由![]() ,
,
得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
(2)由(1)可知![]() .
.
![]() 为直角三角形,
为直角三角形,
又![]() ,
,![]() ,
,
![]() 点在以
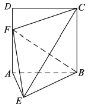
点在以![]() 为直径的圆上,如图,
为直径的圆上,如图,

![]() ,
,![]() ,
,![]() ,
,
设![]() 为
为![]() 中点,连结
中点,连结![]() ,
,
则当点![]() 在
在![]() 上时,
上时,![]() 取得最小值,
取得最小值,
此时,![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在直角![]() 中,
中,![]() ,
,
![]() 当
当![]() 取得最小值
取得最小值![]() 时,
时,![]() 的面积
的面积![]() 为
为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某市为了了解该市教师年龄分布情况,对年龄在![]() 内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
年龄区间 |
|
|
|
|
教师人数 | 2000 | 1300 | ||
样本人数 | 130 |
由于不小心,表格中部分数据被污染,看不清了,统计员只记得年龄在![]() 的样本人数比年龄在
的样本人数比年龄在![]() 的样本人数多10,根据以上信息回答下列问题:
的样本人数多10,根据以上信息回答下列问题:

(1)求该市年龄在![]() 的教师人数;
的教师人数;
(2)试根据上表做出该市教师按照年龄的人数频率分布直方图,并求该市教师年龄的平均数![]() 及方差
及方差![]() (同一组的数据用该组区间的中点值作代表).
(同一组的数据用该组区间的中点值作代表).