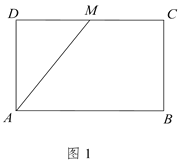
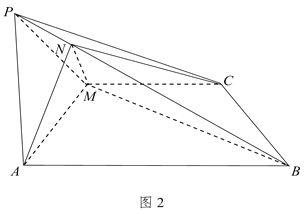
题目内容
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数)
为自然对数的底数)
(1)求![]() 的单调区间;
的单调区间;
(2)已知关于![]() 的方程
的方程![]() 有三个实根,求实数
有三个实根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() 和
和![]() ,无单调递减区间;(2)
,无单调递减区间;(2)![]() .
.
【解析】
(1)求出函数![]() 的定义域和导数,利用导数可求出函数
的定义域和导数,利用导数可求出函数![]() 的单调区间;
的单调区间;
(2)由题意可知,关于![]() 的方程
的方程![]() 在
在![]() 时有三个根,令
时有三个根,令![]() ,利用导数分析函数
,利用导数分析函数![]() 的单调性与极值,利用数形结合思想,结合内层函数与外层函数的零点,对实数
的单调性与极值,利用数形结合思想,结合内层函数与外层函数的零点,对实数![]() 的取值进行分类讨论,分析方程
的取值进行分类讨论,分析方程![]() 的实根个数,从而可得出实数
的实根个数,从而可得出实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,无单调递减区间;
,无单调递减区间;
(2)由![]() ,得
,得![]() ,得
,得![]() .
.
令![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
|
如下图所示,当![]() 时,方程
时,方程![]() 在
在![]() 时有两根,当
时有两根,当![]() 或
或![]() 时,方程
时,方程![]() 在
在![]() 时只有一根.
时只有一根.

作出函数![]() 与函数
与函数![]() 的图象如下图所示:
的图象如下图所示:

①当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,
,
此时方程![]() 在
在![]() 时只有一根,不合乎题意;
时只有一根,不合乎题意;
②当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象有两个交点,横坐标分别为
图象有两个交点,横坐标分别为![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,
方程![]() 在
在![]() 时只有一根,方程
时只有一根,方程![]() 在
在![]() 时只有一根,共有两根,不合乎题意;
时只有一根,共有两根,不合乎题意;
③当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,
,
方程![]() 只有一根,不合乎题意;
只有一根,不合乎题意;
④当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象有两个交点,横坐标分别为
图象有两个交点,横坐标分别为![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,
方程![]() 在
在![]() 时有两根,方程
时有两根,方程![]() 在
在![]() 时只有一根,共有三根,合乎题意;
时只有一根,共有三根,合乎题意;
⑤当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,
,![]() ,
,
方程![]() 在
在![]() 时有一根,方程
时有一根,方程![]() 在
在![]() 时也只有一根,共两根,不合乎题意;
时也只有一根,共两根,不合乎题意;
⑥当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,且
,且![]() ,
,
此时,方程![]() 在
在![]() 时只有一根,不合乎题意.
时只有一根,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率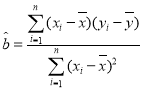 ;相关系数
;相关系数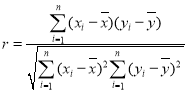 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |