题目内容
【题目】已知中心在原点O,焦点在x轴上的椭圆,离心率 ![]() ,且椭圆过点
,且椭圆过点 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)椭圆左,右焦点分别为F1 , F2 , 过F2的直线l与椭圆交于不同的两点A、B,则△F1AB的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
【答案】解:(Ⅰ)由题意可设椭圆方程为 ![]() .
.
则 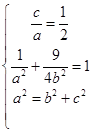 ,解得:a2=4,b2=3.
,解得:a2=4,b2=3.
∴椭圆方程为 ![]() ;
;
(Ⅱ)设A(x1,y1),B(x2,y2),不妨y1>0,y2<0,设△F1AB的内切圆的半径R,
则△F1AB的周长=4a=8, ![]() (|AB|+|F1A|+|F1B|)R=4R,
(|AB|+|F1A|+|F1B|)R=4R,
因此 ![]() 最大,R就最大,
最大,R就最大,
由题知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由 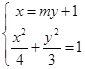 ,得(3m2+4)y2+6my﹣9=0,
,得(3m2+4)y2+6my﹣9=0,
![]() .
.
则 ![]() =
= ![]() ,
,
令 ![]() ,则m2=t2﹣1,
,则m2=t2﹣1,
∴ ![]() =
=  ,
,
令f(t)=3t+ ![]() ,则f′(t)=3﹣
,则f′(t)=3﹣ ![]() ,
,
当t≥1时,f′(t)≥0,f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4, ![]() ≤3,
≤3,
即当t=1,m=0时, ![]() ≤3,
≤3,
由 ![]() =4R,得Rmax=
=4R,得Rmax= ![]() ,这时所求内切圆面积的最大值为
,这时所求内切圆面积的最大值为 ![]() .
.
故直线l:x=1,△F1AB内切圆面积的最大值为 ![]() .
.
【解析】(Ⅰ)设椭圆方程,由题意列关于a,b,c的方程组求解a,b,c的值,则椭圆方程可求;(Ⅱ)设A(x1,y1),B(x2,y2),不妨设y1>0,y2<0,设△F1AB的内切圆的径R,则△F1AB的周长=4a=8, ![]() =
= ![]() (|AB|+|F1A|+|F1B|)R=4R,因此
(|AB|+|F1A|+|F1B|)R=4R,因此 ![]() 最大,R就最大.设直线l的方程为x=my+1,与椭圆方程联立,从而可表示△F1AB的面积,利用换元法,借助于导数,即可求得结论.
最大,R就最大.设直线l的方程为x=my+1,与椭圆方程联立,从而可表示△F1AB的面积,利用换元法,借助于导数,即可求得结论.

 阅读快车系列答案
阅读快车系列答案【题目】某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为 ![]() ,C、D两辆汽车每天出车的概率均为
,C、D两辆汽车每天出车的概率均为 ![]() ,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
【题目】漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资. (Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
雕刻量n | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.