Question

【题目】某厂生产一种机器的固定成本为0.5万元，但每生产100台，需要加可变成本（即另增加投入）0.25万元，市场对此产品的年求量为500台，销售的收入函数为（万元）（），其中是产品售出的数量（单位：百台）.

（1）把利润表示为年产量的函数；

（2）年产量是多少时，工厂所得利润最大？

Answer 1

【答案】（1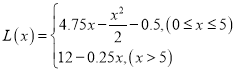）；（2）生产475台所得利润最大.

【解析】

（1）根据题意，分和两种情况进行讨论，分别根据利润＝销售收入成本，列出函数关系，即可得到利润表示为年产量的函数；
（2）根据（1）所得的分段函数，分类讨论，分别求出两段函数的最值，然后进行比较，即可得到答案；

解：（1）当时，产品能售出百台；

当时，只能售出5百台，这时，成本为万元，

依题意可得利润函数为

.

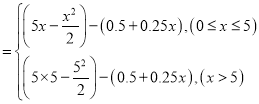即.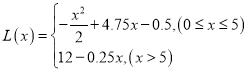

（2）当时，，
∵抛物线开口向下，对称轴为，
∴当时，；
当时，为上的减函数，
．
综合得，当时，取最大值，
∴年产量为475台时，工厂利润最大．