题目内容
14. 如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.
如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.(1)当三棱椎B1-BEF的体积最大时,求二面角B1-EF-B的正切值;
(2)求异面直线A1E与B1F所成的角的取值范围.
分析 (1)由已知得${V}_{{B}_{1}-BEF}=\frac{1}{3}×\frac{1}{2}×(a-x)×x×a$=$\frac{a}{6}(a-x)x$≤$\frac{a}{6}(\frac{a-x+x}{2})^{2}$=$\frac{{a}^{3}}{24}$,从而当x=$\frac{a}{2}$时,三棱锥B1-BEF的体积最大.取EF中点O,则∠B1OB是二面角B1-EF-B的平面角,由此能求出当三棱椎B1-BEF的体积最大时,二面角B1-EF-B的正切值.
(2)在AD上取点H,使AH=BF=AE,则HF∥CD∥A1B1,A1H∥B1F,从而∠HA1E(或补角)是异面直线A1E与B1F所成的角,由此利用余弦定理能求出异面直线A1E与B1F所成的角的取值范围.
解答 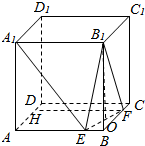 解:(1)∵正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x,
解:(1)∵正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x,
∴${V}_{{B}_{1}-BEF}=\frac{1}{3}×\frac{1}{2}×(a-x)×x×a$=$\frac{a}{6}(a-x)x$≤$\frac{a}{6}(\frac{a-x+x}{2})^{2}$=$\frac{{a}^{3}}{24}$,
∴当a-x=x,即x=$\frac{a}{2}$时,三棱锥B1-BEF的体积最大.
取EF中点O,∵BO⊥EF,B1O⊥EF,∴∠B1OB是二面角B1-EF-B的平面角.
在Rt△BEF中,BO=$\frac{1}{2}EF$=$\frac{1}{2}×\frac{\sqrt{2}}{2}a$=$\frac{\sqrt{2}}{4}$a,
∴tan∠B1OB=$\frac{B{B}_{1}}{BO}$=$\frac{a}{\frac{\sqrt{2}}{4}a}$=2$\sqrt{2}$.
∴当三棱椎B1-BEF的体积最大时,二面角B1-EF-B的正切值为$2\sqrt{2}$.
(2)在AD上取点H,使AH=BF=AE,则HF∥CD∥A1B1,
∵HF=CD=A1B1,A1H∥B1F,∴∠HA1E(或补角)是异面直线A1E与B1F所成的角,
在Rt△A1AH中,${A}_{1}H=\sqrt{{a}^{2}+{x}^{2}}$,在Rt△A1AE中,${A}_{1}E=\sqrt{{a}^{2}+{x}^{2}}$,
在Rt△HAE中,HE=$\sqrt{{x}^{2}+{x}^{2}}$=$\sqrt{2}x$,
在△HA1E中,cos∠HA1E=$\frac{{A}_{1}{H}^{2}+{A}_{1}{E}^{2}-E{H}^{2}}{2•{A}_{1}H•{A}_{1}E}$=$\frac{{a}^{2}}{{a}^{2}+{x}^{2}}$,
∵0<x≤a,∴a2<x2+a2≤2a2,$\frac{1}{2}≤\frac{{a}^{2}}{{x}^{2}+{a}^{2}}<1$,
∴$\frac{1}{2}≤cos∠H{A}_{1}E<1$,
∴异面直线A1E与B1F所成的角的取值范围是[$\frac{1}{2}$,1).
点评 本题考查三棱椎的体积最大时,二面角的正切值的求法,考查异面直线所成的角的取值范围的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用和空间思维能力的培养.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
| A. | $\frac{4}{3}π$ | B. | $\frac{2}{3}π$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
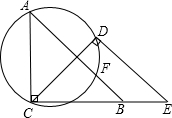 已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.
已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心. 如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.
如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.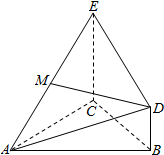 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.