题目内容
19．三棱锥的三条侧棱两两垂直，3个侧面与底面所成的角分别为30°、45°、60°，底面面积为$\sqrt{6}$，求三棱锥的体积．分析 设S到底面的距离SH=h，连接AH，BH，CH延长交对边于D，E，F，连接SD，SE，SF，由SA，SB，SC两两垂直，可得H为垂心，由线面垂直的判断和性质，可得3个侧面与底面所成的角，再由解直角三角形，可得h的关系式，运用等积法，可得h，进而得到体积．
解答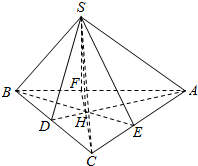 
解：设三棱锥S-ABC三侧棱长分别为SA=x，SB=y，SC=z，
S到底面的距离SH=h，
连接AH，BH，CH延长交对边于D，E，F，
连接SD，SE，SF，
由SA，SB，SC两两垂直，可得H为垂心，
由线面垂直的性质定理，SD⊥BC，SE⊥AC，SF⊥AB，
即有∠SDA=30°，∠SEB=45°，∠SFC=60°，
在直角三角形SAD中，SA=x=$\frac{h}{cos30°}$，
同理可得SB=y=$\frac{h}{cos45°}$，SC=z=$\frac{h}{cos60°}$，
由体积公式可得，VS-ABC=VB-SAC，
即为$\frac{1}{3}$•$\frac{1}{2}$xyz=$\frac{1}{3}$•h•$\sqrt{6}$，
代入化简可得h=$\frac{\sqrt{6}}{2}$，
则三棱锥的体积为$\frac{1}{3}$•h•$\sqrt{6}$=1．
点评 本题考查空间二面角的求法和棱锥体积的计算，考查线面位置关系，考查运算能力，属于中档题．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=4，BC=3，沿对角线AC把矩形折成二面角D-AC-B，并且D点在平面ABC内的射影落在AB上．
如图，正方体ABCD=A1B1C1D1，棱长为a，E、F分别为AB、BC上的点，且AE=BF=x．
11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率e∈[$\sqrt{2}$，2]，则其渐近线的倾斜角的取值范围是（ ）
| A． | [$\frac{π}{4}$，$\frac{π}{3}$]∪[$\frac{2π}{3}$，$\frac{3π}{4}$] | B． | [$\frac{π}{6}$，$\frac{π}{3}$]∪[$\frac{2π}{3}$，$\frac{5π}{6}$] | C． | [$\frac{π}{6}$，$\frac{π}{4}$]∪[$\frac{4π}{3}$，$\frac{5π}{6}$] | D． | [$\frac{π}{4}$，$\frac{π}{3}$]∪[$\frac{2π}{3}$，$\frac{5π}{5}$] |