Question

4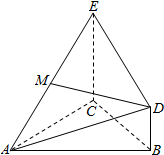．如图，△ABC为正三角形，EC⊥平面ABC，BD∥CE且CE=CA=2BD，M是EA的中点．
（Ⅰ）证明：DM∥平面ABC；
（Ⅱ）若正三角形ABC的边长是a，求三棱锥D-ECA的体积．

Answer 1

分析 （Ⅰ）取AC的中点N，连接MN，BN，利用三角形中位线定理与平行四边形的判定与性质定理可得DM∥BN，再利用线面平行的判定定理可得：DM∥平面ABC．
（Ⅱ）证明DM⊥平面AEC，利用体积公式求三棱锥D-ECA的体积．

解答 （Ⅰ）证明：取AC的中点N，连接MN，BN
∵M是AE的中点，∴MN∥CE，CE=2MN，
∵CE∥BD，CE=2BD，
∴MN∥BD，MN=BD
∴四边形BDMN为平行四边形，
∴DM∥BN，DM?平面ABC，BN?平面ABC，
∴DM∥平面ABC．
（Ⅱ）解：∵△ABC是正三角形，
∴BN⊥AC，
∵EC⊥平面ABC，
∴BN⊥CE，
∴BN⊥平面ACE，
∵BN∥DM，
∴DM⊥平面AEC，
∴V_D-ECA=$\frac{1}{3}×\frac{1}{2}{a}^{2}×\frac{\sqrt{3}}{2}a$=$\frac{\sqrt{3}}{12}{a}^{3}$．

点评 本题考查了线面平行的判定定理、三角形的中位线定理、棱锥的体积计算公式、平行四边形的判定与性质定理，考查了推理能力与计算能力，属于中档题．