题目内容
14.设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.(1)求证:函数f(x)恒有f(x+4)=f(x)成立;
(2)x∈[2,4],求f(x)的解析式;
(3)计算f(0)+f(1)+f(2)+…+f(2015).
分析 (1)由题意可得f(x)=-f(x+2)=-(-f(x+4))=f(x+4);
(2)由[0,2]上的表达式先求[-2,0]上的表达式,再求[2,4]上的表达式;
(3)由周期性可化为f(0)+f(1)+f(2)+…+f(2015)=504[f(0)+f(1)+f(2)+f(-1)],再由奇偶性求解.
解答 (1)证明:∵f(x+2)=-f(x),
∴f(x)=-f(x+2)=-(-f(x+4))=f(x+4);
(2)解:∵当x∈[0,2]时,f(x)=2x-x2,
又∵f(x)是定义在R上的奇函数,
∴x∈[-2,0]时,f(x)=2x+x2,
故当x∈[2,4]时,f(x)=f(x-4)
=2(x-4)+(x-4)2
=x2-6x+8;
(3)解:∵f(x+4)=f(x),
∴f(x)是以4为周期的周期函数;
∴f(0)+f(1)+f(2)+…+f(2015)
=504[f(0)+f(1)+f(2)+f(3)]
=504[f(0)+f(1)+f(2)+f(-1)]
=0.
点评 本题考查了抽象函数的周期性与奇偶性的判断与应用,同时考查了函数解析式的求法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

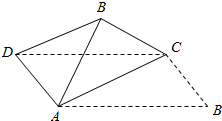 如图,将矩形纸片ABCD(其中
如图,将矩形纸片ABCD(其中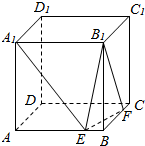 如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.
如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.