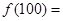题目内容
设 是连续的偶函数,且当
是连续的偶函数,且当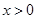 时
时 是单调函数,则满足
是单调函数,则满足 的所有
的所有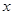 之和为( )
之和为( )
 是连续的偶函数,且当
是连续的偶函数,且当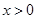 时
时 是单调函数,则满足
是单调函数,则满足 的所有
的所有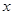 之和为( )
之和为( )A.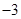 | B.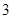 | C. | D.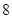 |
C
试题分析:根据已知函数
 是连续的偶函数,且当
是连续的偶函数,且当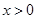 时
时 是单调函数,且有
是单调函数,且有 ,则说明而来
,则说明而来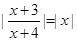 ,那么解方程可知满足方程的解
,那么解方程可知满足方程的解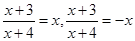 求解得到方程的根满足
求解得到方程的根满足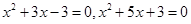 ,那么结合韦达定理可知四个根的和为-8,故选C.
,那么结合韦达定理可知四个根的和为-8,故选C.点评:对于方程根的求解,要结合函数的偶函数性质的对称性质,以及函数的单调性来分析得到结论,属于基础题。

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
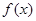 表示学生注意力随时间
表示学生注意力随时间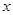 (分钟)的变化规律(
(分钟)的变化规律(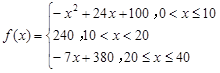
 ,则
,则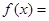 。
。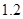 万件、
万件、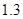 万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量
万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量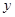 与月份
与月份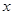 的关系,模拟函数可选用函数
的关系,模拟函数可选用函数 (其中
(其中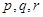 为常数)或二次函数。又已知当年4月份该产品的产量为
为常数)或二次函数。又已知当年4月份该产品的产量为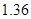 万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
万件,请问用以上哪个函数作为模拟函数较好,并说明理由。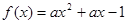 在
在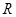 上恒满足
上恒满足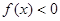 ,则
,则 的取值范围是
的取值范围是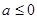

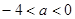

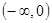 上是增函数的是( )
上是增函数的是( )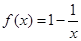
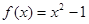
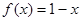
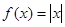
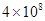 米)
米)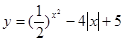 的一个单调减区间为_______.
的一个单调减区间为_______.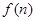 是定义在自然数集上的函数,
是定义在自然数集上的函数,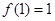 ,且对任意自然数
,且对任意自然数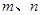 ,有
,有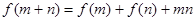 ,则
,则