题目内容
已知抛物线 (
( )的焦点
)的焦点 为双曲线
为双曲线 (
( )的一个焦点,经过两曲线交点的直线恰过点
)的一个焦点,经过两曲线交点的直线恰过点 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A. | B.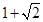 | C. | D. |
B
解析试题分析:抛物线 (
( )的焦点
)的焦点 ,它也是双曲线
,它也是双曲线 (
( )的一个焦点,所以有
)的一个焦点,所以有 ①,由两曲线交点的直线恰过点
①,由两曲线交点的直线恰过点 ,可知它们在第一象限的交点为
,可知它们在第一象限的交点为 ,此点也在双曲线上,故有
,此点也在双曲线上,故有 ②,由①②消去
②,由①②消去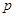 ,得
,得 ,即
,即 ,即
,即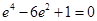 ,因为
,因为 ,所以
,所以 ,选择B,求离心率的值关键是寻找到关于
,选择B,求离心率的值关键是寻找到关于 的等式,然后转化到
的等式,然后转化到 的方程,从而解出
的方程,从而解出 .
.
考点:圆锥曲线的性质

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
| A.直线 | B.圆 | C.抛物线 | D.双曲线 |
已知 是抛物线
是抛物线 的焦点,
的焦点, 是该抛物线上的两点.若线段
是该抛物线上的两点.若线段 的中点到
的中点到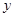 轴的距离为
轴的距离为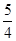 ,则
,则 ( )
( )
| A.2 | B. | C.3 | D.4 |
设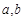 是关于t的方程
是关于t的方程 的两个不等实根,则过
的两个不等实根,则过 ,
, 两点的直线与双曲线
两点的直线与双曲线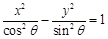 的公共点的个数为( )
的公共点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
若双曲线 的离心率为
的离心率为 ,则其渐近线的斜率为( )
,则其渐近线的斜率为( )
A. | B. | C.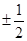 | D. |
双曲线 与椭圆
与椭圆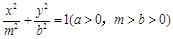 的离心率互为倒数,则( )
的离心率互为倒数,则( )
A. | B. | C. | D. |
已知点A(3,4),F是抛物线y2=8x的焦点,M是抛物线上的动点,当|AM|+|MF|最小时,M点坐标是( )
| A.(0,0) | B.(3,2 ) ) | C.(2,4) | D.(3,-2 ) ) |
 的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且
的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ). B.
B. C.
C.  D.
D.
 ,
, 且圆心在
且圆心在 轴
轴
 上的圆的方程.
上的圆的方程.