题目内容
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
| A.直线 | B.圆 | C.抛物线 | D.双曲线 |
B
解析试题分析:由已知得 即
即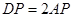 ,在平面ABCD内以AD所在直线为x轴,AD中点为坐标原点建立直角坐标系,设A(1,0),B(-1,0),P(x,y),由
,在平面ABCD内以AD所在直线为x轴,AD中点为坐标原点建立直角坐标系,设A(1,0),B(-1,0),P(x,y),由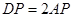 建立等式化简得轨迹方程为
建立等式化简得轨迹方程为 ,是圆的一般方程,所以答案选B。
,是圆的一般方程,所以答案选B。
考点:1.直角三角形中的三角函数定义;2.轨迹方程的求解

练习册系列答案
相关题目
已知抛物线 的准线与双曲线
的准线与双曲线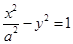
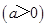 交于
交于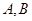 两点,点
两点,点 为抛物线的焦点,若
为抛物线的焦点,若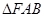 为直角三角形,则双曲线的离心率是( )
为直角三角形,则双曲线的离心率是( )
A.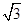 | B. | C.2 | D.3 |
直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( )
A.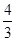 | B.2 | C.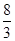 | D.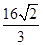 |
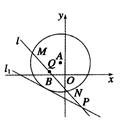
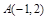 为圆心的圆与直线
为圆心的圆与直线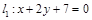 相切.过点
相切.过点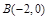 的动直线
的动直线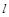 与圆
与圆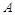 相交于
相交于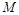 ,
,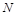 两点,
两点,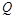 是
是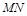 的中点,直线
的中点,直线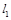 相交于点
相交于点 .
.
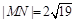 时,求直线
时,求直线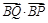 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.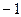 , 0),B(0, 2)的直线
, 0),B(0, 2)的直线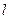 与圆
与圆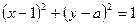 相切,求
相切,求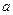 的值
的值
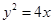 的准线与双曲线
的准线与双曲线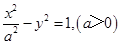 交于A,B两点,点F为抛物线的焦点,若
交于A,B两点,点F为抛物线的焦点,若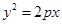 (
( )的焦点
)的焦点 为双曲线
为双曲线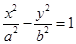 (
(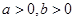 )的一个焦点,经过两曲线交点的直线恰过点
)的一个焦点,经过两曲线交点的直线恰过点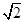
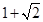
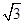


 过圆O上任P一点作y轴的垂线,垂足为Q,求线段PQ的中点M的轨迹方程。(12分)
过圆O上任P一点作y轴的垂线,垂足为Q,求线段PQ的中点M的轨迹方程。(12分)