题目内容
1.f(x)=3x2-6x-5,(1)设g(x)=f(x)-2x2+mx,其中m∈R,求g(x)在[1,3]上的最大值.
(2)若对任意的a∈[-1,2]存在x∈[1,3],使不等式f(x)≤x2-(2a+6)x+a+b成立,求实数b的取值范围.
分析 (1)分析g(x)的图象和性质,分析对称轴与给定区间的关系,可得g(x)在[1,3]上的最大值.
(2)若对任意的a∈[-1,2]存在x∈[1,3],使不等式f(x)≤x2-(2a+6)x+a+b成立,则对任意的a∈[-1,2],函数y=2x2+2ax-5-a-b最大值不大于0,结合二次函数的图象和性质,可得实数b的取值范围.
解答 解:(1)∵f(x)=3x2-6x-5,
∴g(x)=f(x)-2x2+mx=x2+(m-6)x-5,
∵g(x)的图象是开口朝上,且以x=3-$\frac{m}{2}$为对称轴的抛物线,
故当3-$\frac{m}{2}$≥2,即m≤2时,g(x)在[1,3]上的最大值为g(3)=3m-14;
当3-$\frac{m}{2}$<2,即m>2时,g(x)在[1,3]上的最大值为g(1)=m-10;
(2)对任意的a∈[-1,2],存在x∈[1,3],使不等式f(x)≤x2-(2a+6)x+a+b成立,
即2x2+2ax-5-a-b≤0成立,
故对任意的a∈[-1,2],函数y=2x2+2ax-5-a-b最大值不大于0,
由函数y=2x2+2ax-5-a-b的图象是开口朝上,且以直线x=-$\frac{a}{2}$为对称轴的抛物线,-$\frac{a}{2}$∈[-$\frac{1}{2}$,1],
故函数y=2x2+2ax-5-a-b在[1,3]上为增函数,
当x=3时,函数取最大值5a-b+13,
故5a-b+13≤0,
即b≥5a+13,a∈[-1,2]
故b≥23
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
16.算法如果执行下面的程序框图,输入n=6,m=4,那么输出的p于( )
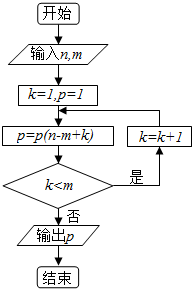

| A. | 12 | B. | 60 | C. | 360 | D. | 48 |
10.定义在(0,$\frac{π}{2}$)上的函数f(x),其导函数f′(x)在(0,$\frac{π}{2}$)上总使得f(x)<f′(x)•tanx成立,则下列各式中一定成立的是( )
| A. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | B. | f($\frac{π}{6}$)<$\sqrt{3}$f($\frac{π}{3}$) | C. | $\sqrt{3}$f($\frac{π}{6}$)>f($\frac{π}{3}$) | D. | $\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$) |
10.已知集合S={(x,y)|x+y=4},T={(x,y)|x-y=2},那么集合S∩T=( )
| A. | {3,1} | B. | (3,1) | C. | x=3,y=1 | D. | {(3,1)} |
 ,各项
,各项 ,公比为
,公比为 .(1)设
.(1)设 ,求证:
,求证: 是等差数列,并求出该数列的首项
是等差数列,并求出该数列的首项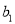 及公差
及公差 ;
; 的取值范围.
的取值范围.