题目内容
10.定义在(0,$\frac{π}{2}$)上的函数f(x),其导函数f′(x)在(0,$\frac{π}{2}$)上总使得f(x)<f′(x)•tanx成立,则下列各式中一定成立的是( )| A. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | B. | f($\frac{π}{6}$)<$\sqrt{3}$f($\frac{π}{3}$) | C. | $\sqrt{3}$f($\frac{π}{6}$)>f($\frac{π}{3}$) | D. | $\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$) |
分析 把给出的等式变形得到f′(x)sinx-f(x)cosx>0,由此联想构造辅助函数g(x)=$\frac{f(x)}{sinx}$,由其导函数的符号得到其在(0,$\frac{π}{2}$)上为增函数,则g($\frac{π}{6}$)<g($\frac{π}{3}$),整理后即可得到答案.
解答 解:∵x∈(0,$\frac{π}{2}$),∴sinx>0,cosx>0.
由f(x)<f′(x)tanx,得f(x)cosx<f′(x)sinx,
即f′(x)sinx-f(x)cosx>0.
令g(x)=$\frac{f(x)}{sinx}$,x∈(0,$\frac{π}{2}$),则g′(x)=$\frac{f′(x)sinx-f(x)cosx}{si{n}^{2}x}$>0.
∴函数g(x)=$\frac{f(x)}{sinx}$在x∈(0,$\frac{π}{2}$)上为增函数,
则g($\frac{π}{6}$)<g($\frac{π}{3}$),即$\frac{f(\frac{π}{6})}{sin\frac{π}{6}}<\frac{f(\frac{π}{3})}{sin\frac{π}{3}}$,
∴$\frac{f(\frac{π}{6})}{\frac{1}{2}}<\frac{f(\frac{π}{3})}{\frac{\sqrt{3}}{2}}$,
即$\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$).
故选:D.
点评 本题考查了导数的运算法则,考查了利用函数导函数的符号判断函数的单调性,考查了函数构造法,属中档题.

练习册系列答案
相关题目
1. 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
(Ⅰ)完成频率分布表,并画出频率分布直方图;
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.| 分组 | 频数 | 频率 |
| [1.30,1.34) | 4 | |
| [1.34,1.38) | 25 | |
| [1.38,1.42) | 30 | |
| [1.42,1.46) | 29 | |
| [1.46,1.50) | 10 | |
| [1.50,1.54) | 2 | |
| 合计 | 100 |
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
18.函数y=$\sqrt{{x}^{2}-4x+13}$-$\sqrt{{x}^{2}+1}$的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 10 | C. | $\sqrt{10}$ | D. | 0 |
5.下列关系中正确的个数为( )
①$\frac{1}{2}$∈R ②$\sqrt{2}$∉Q ③|-3|∉N+ ④|-$\sqrt{3}$|∈Q.
①$\frac{1}{2}$∈R ②$\sqrt{2}$∉Q ③|-3|∉N+ ④|-$\sqrt{3}$|∈Q.
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
15.下列说法正确的是( )
| A. | 命题“若幂函数f(x)=xa在(0,+∞)内单调递减,则 a<0”的逆否命题是“若a≥0,则幂函数f(x)=xa在(0,+∞)内单调递增” | |
| B. | 已知命题p 和q,若p∧q为假命题,则命题p、q中必有一个是真命题、一个是假命题 | |
| C. | 若x,y∈R,则“x=y”是“$xy≥{(\frac{x+y}{2})^2}$”的充要条件 | |
| D. | 若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1>0 |
 的首项
的首项 ,前
,前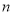 项和为
项和为 ,且
,且 ,则数列
,则数列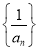 的前5项和为( )
的前5项和为( ) B.
B.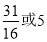 C.
C. D.
D.