题目内容
10.已知集合S={(x,y)|x+y=4},T={(x,y)|x-y=2},那么集合S∩T=( )| A. | {3,1} | B. | (3,1) | C. | x=3,y=1 | D. | {(3,1)} |
分析 根据交集的定义,S∩T的元素同时满足x+y=4和x-y=2,从而解$\left\{\begin{array}{l}{x+y=4}\\{x-y=2}\end{array}\right.$即可得出x,y,从而得出集合S∩T的元素,从而得出S∩T.
解答 解:解$\left\{\begin{array}{l}{x+y=4}\\{x-y=2}\end{array}\right.$得,$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$;
∴S∩T={(3,1)}.
故选:D.
点评 考查交集的定义,描述法、列举法表示集合,有序数对(x,y)表示元素,注意交集是一个集合.

练习册系列答案
相关题目
5.已知f(x-1)=x2+6x,则f(x)的表达式是( )
| A. | x2+4x-5 | B. | x2+8x+7 | C. | x2+2x-3 | D. | x2+6x-10 |
15.设θ是第三象限角,|cos$\frac{θ}{2}$|=cos$\frac{θ}{2}$,则$\frac{θ}{2}$是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 的首项
的首项 ,前
,前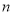 项和为
项和为 ,且
,且 ,则数列
,则数列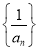 的前5项和为( )
的前5项和为( ) B.
B.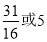 C.
C. D.
D.