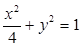题目内容
(本题满分10分)
在极坐标系中,已知两点O(0,0),B(2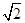 ,
,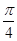 ).
).

(Ⅰ)求以OB为直径的圆C的极坐标方程,然后化成直角坐标方程;
(Ⅱ)以极点O为坐标原点,极轴为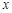 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为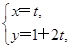 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
在极坐标系中,已知两点O(0,0),B(2
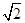 ,
,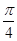 ).
).
(Ⅰ)求以OB为直径的圆C的极坐标方程,然后化成直角坐标方程;
(Ⅱ)以极点O为坐标原点,极轴为
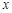 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为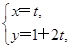 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.(1) (x-1)2+(y-1)2="2" (2)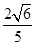
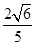
试题分析:解: (Ⅰ)设P(r,q)为圆上任意一点,则|OP|=r,ÐPOx=q-
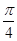 ,
,在RtDPOB中,cos(q-
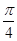 )=
)= ,即r=2
,即r=2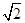 cos(q-
cos(q-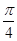 ).
).∴r2=2
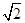 rcosq×
rcosq×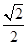 +2
+2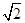 rsinq×
rsinq×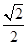 ,
,∴圆C的直角坐标方程为(x-1)2+(y-1)2=2. ……5分
(Ⅱ)作CD^MN于D,C到直线l的距离为d=
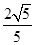 ,
,在RtDCDA中,|MN|=2
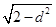 =
=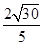 ,
,∴S=
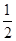 ×
×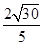 ×
×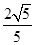 =
=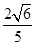 . ……10分
. ……10分点评:熟练掌握极坐标与直角坐标的互化,同时能利用直线与圆的位置关系,利用圆的半径,点到直线的距离公式以及弦长的关系来求解,并结合三角形正弦面积公式得到,属于中档题。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目


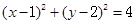 关于
关于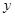 轴对称的圆的方程为______________.
轴对称的圆的方程为______________.  与圆
与圆 的两个交点,则
的两个交点,则 ( )
( ) D.
D.
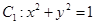 ,圆
,圆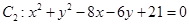 ,则两圆公切线的条数有( )
,则两圆公切线的条数有( )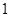 条
条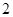 条
条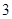 条
条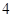 条
条 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )



 ,若线段
,若线段 是△
是△ 外接圆的直径,则点
外接圆的直径,则点 的坐标是( ).
的坐标是( ). 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,它的长轴长等于圆
,它的长轴长等于圆 的半径,则椭圆的标准方程是( )
的半径,则椭圆的标准方程是( )