题目内容
如图所示,已知点P是⊙O外一点,PS、PT是⊙O的两条切线,过点P作⊙O
的割线PAB,交⊙O于A、B两点,与ST交于点C,求证:

的割线PAB,交⊙O于A、B两点,与ST交于点C,求证:


利用切割线定理再由三角形相似即可证.
试题分析:作OD垂直PB于D,连接SD、OS、PO,则有P、S、D、O四点共圆,PA+PB=2PD,又由切割线定理可知PS2=PA·PB,又易证三角形PSC与三角形PCS相似可得,PS2=PC·PD,即有
PC·PD=PC·
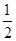 (PA+PB)=PA·PB,从而得证.
(PA+PB)=PA·PB,从而得证.点评:本题主要考查了切割线定理以及三角形相似的证明,注意对比例式的变形是解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
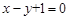 上,且经过圆
上,且经过圆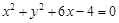 与圆
与圆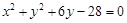 的交点的圆方程.
的交点的圆方程.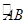 =
=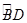 ,过C点的圆的切线与BA的延长线交于E点
,过C点的圆的切线与BA的延长线交于E点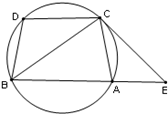
 的圆心坐标为
的圆心坐标为 ,则实数
,则实数 .
.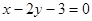 与圆
与圆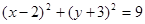 交于
交于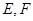 两点,则
两点,则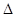
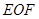 (
(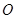 是原点)的面积为
是原点)的面积为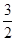
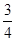
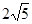
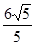
 (a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知|
(a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知| |·|
|·| |的最小值为m.当
|的最小值为m.当 ≤m≤
≤m≤ 时,其中c=
时,其中c= ,则双曲线的离心率e的取值范围是 ( )
,则双曲线的离心率e的取值范围是 ( )


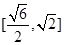
 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 为切点,
为切点, .若
.若 ,
, ,则
,则 的长为 .
的长为 . 
 交x轴于A,B两点,曲线C是以AB为长轴,离心率为
交x轴于A,B两点,曲线C是以AB为长轴,离心率为 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点P作直线PF的垂线交直线
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点P作直线PF的垂线交直线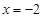 于点Q.
于点Q.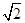 ,
,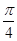 ).
).
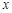 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为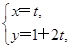 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.