题目内容
如图,圆锥的高PO=4,底面半径OB=2,D为PO的中点,E为母线PB的中点,F为底面圆周上一点,满足EF⊥DE.
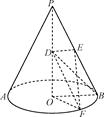
(1)求异面直线EF与BD所成角的余弦值;
(2)求二面角OOFE的正弦值.

(1)求异面直线EF与BD所成角的余弦值;
(2)求二面角OOFE的正弦值.
(1)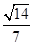 (2)
(2)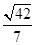
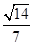 (2)
(2)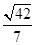
(1)以O为原点,底面上过O点且垂直于OB的直线为x轴,OB所在的线为y轴,OP所在的线为z轴,建立空间直角坐标系,则
B(0,2,0),P(0,0,4),D(0,0,2),E(0,1,2).
设F(x0,y0,0)(x0>0,y0>0),且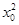 +
+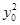 =4,
=4,
则 =(x0,y0-1,-2),
=(x0,y0-1,-2),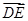 =(0,1,0),
=(0,1,0),
∵EF⊥DE,即 ⊥
⊥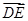 ,则
,则 ·
·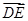 =y0-1=0,故y0=1.
=y0-1=0,故y0=1.
∴F(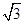 ,1,0),
,1,0), =(
=(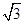 ,0,-2),
,0,-2),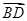 =(0,-2,2).
=(0,-2,2).
设异面直线EF与BD所成角为α,则cosα=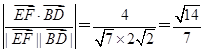 .
.
(2)设平面ODF的法向量为n1=(x1,y1,z1),则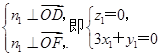
令x1=1,得y1=-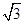 ,平面ODF的一个法向量为n1=(1,-
,平面ODF的一个法向量为n1=(1,-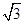 ,0).
,0).
设平面DEF的法向量为n2=(x2,y2,z2),
同理可得平面DEF的一个法向量为n2=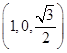 .
.
设二面角ODFE的平面角为β,则|cosβ|=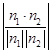 =
=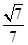 .
.
∴sinβ=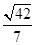 .
.
B(0,2,0),P(0,0,4),D(0,0,2),E(0,1,2).
设F(x0,y0,0)(x0>0,y0>0),且
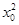 +
+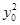 =4,
=4,则
 =(x0,y0-1,-2),
=(x0,y0-1,-2),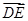 =(0,1,0),
=(0,1,0),∵EF⊥DE,即
 ⊥
⊥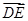 ,则
,则 ·
·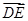 =y0-1=0,故y0=1.
=y0-1=0,故y0=1.∴F(
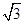 ,1,0),
,1,0), =(
=(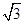 ,0,-2),
,0,-2),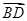 =(0,-2,2).
=(0,-2,2).设异面直线EF与BD所成角为α,则cosα=
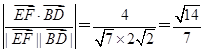 .
.(2)设平面ODF的法向量为n1=(x1,y1,z1),则
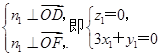
令x1=1,得y1=-
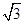 ,平面ODF的一个法向量为n1=(1,-
,平面ODF的一个法向量为n1=(1,-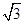 ,0).
,0).设平面DEF的法向量为n2=(x2,y2,z2),
同理可得平面DEF的一个法向量为n2=
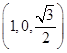 .
.设二面角ODFE的平面角为β,则|cosβ|=
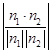 =
=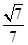 .
.∴sinβ=
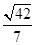 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的点.
上的点.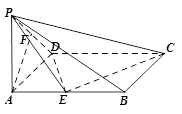
 是
是 的中点时,求证:
的中点时,求证: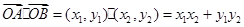 平面
平面 ;
;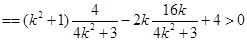 的大小为
的大小为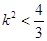 ,试确定
,试确定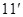 点的位置.
点的位置.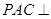 平面
平面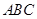 ,
,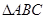 是以
是以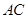 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,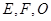 分别为
分别为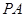 ,
,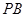 ,
,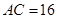 ,
,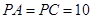 .
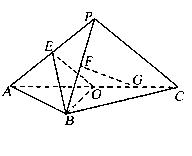
.
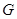 是
是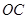 的中点,证明:
的中点,证明: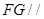 平面
平面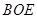 ;
;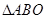 内存在一点
内存在一点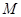 ,使
,使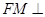 平面
平面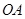 ,
,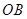 的距离.
的距离.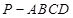 中,
中,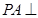 面
面 ,
,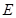 、
、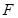 分别为
分别为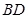 、
、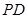 的中点,
的中点,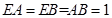 ,
,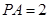 .
.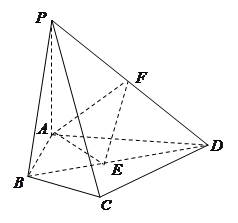
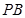 ∥面
∥面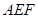 ;
;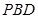 与面
与面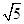 ,AB=AD=
,AB=AD=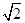 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).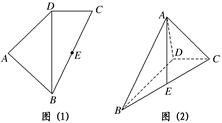
 、
、 满足
满足 ,且
,且 的夹角为
的夹角为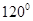 ,则
,则 ;
;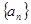 的前
的前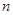 项和为
项和为 ,则
,则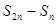 、
、 也成等比数列;
也成等比数列;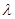 ,使得
,使得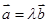 成立。
成立。 ,则
,则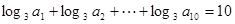
 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.