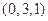题目内容
在正方体ABCDA1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
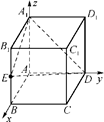

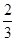
以A为原点建立平面直角坐标系,设棱长为1,则A1(0,0,1),E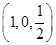 ,D(0,1,0),∴
,D(0,1,0),∴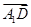 =(0,1,-1),
=(0,1,-1),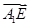 =
=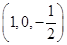 ,
,
设平面A1ED的法向量为n1=(1,y,z),
则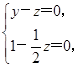 ∴
∴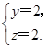 ∴n1=(1,2,2).∵平面ABCD的一个法向量为n2=(0,0,1),∴cos〈n1,n2〉=
∴n1=(1,2,2).∵平面ABCD的一个法向量为n2=(0,0,1),∴cos〈n1,n2〉=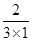 =
=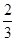 .即所成的锐二面角的余弦值为
.即所成的锐二面角的余弦值为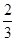 .
.
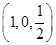 ,D(0,1,0),∴
,D(0,1,0),∴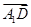 =(0,1,-1),
=(0,1,-1),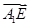 =
=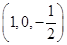 ,
,设平面A1ED的法向量为n1=(1,y,z),
则
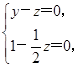 ∴
∴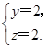 ∴n1=(1,2,2).∵平面ABCD的一个法向量为n2=(0,0,1),∴cos〈n1,n2〉=
∴n1=(1,2,2).∵平面ABCD的一个法向量为n2=(0,0,1),∴cos〈n1,n2〉=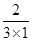 =
=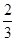 .即所成的锐二面角的余弦值为
.即所成的锐二面角的余弦值为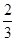 .
.
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
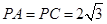 ,
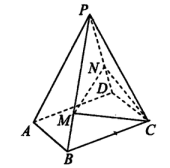
,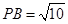 ,M、N两点分别在侧棱PB、PD上,
,M、N两点分别在侧棱PB、PD上,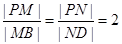 .
.
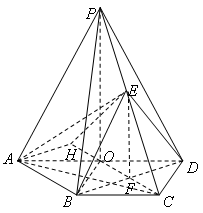
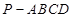 中,底面
中,底面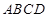 是直角梯形,
是直角梯形,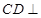 平面
平面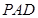 ,
,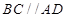 ,
,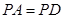 ,
,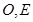 分别为
分别为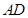 ,
,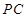 的中点,
的中点,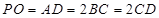 .
.
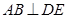 ;
;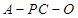 的余弦值.
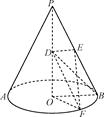
的余弦值. 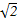 ,☉O的直径AB=2,C是
,☉O的直径AB=2,C是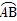 的中点,D为AC的中点.
的中点,D为AC的中点.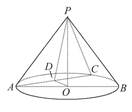

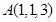 与点
与点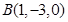 的距离为 .
的距离为 .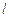 的方向向量为
的方向向量为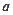 ,平面
,平面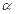 的法向量为
的法向量为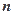 ,则能使
,则能使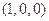 ,
,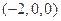
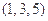 ,
,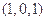
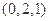 ,
,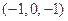
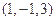 ,
,