题目内容
(本小题满分12分)
已知⊙ 的圆心
的圆心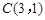 ,被
,被 轴截得的弦长为
轴截得的弦长为 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若圆 与直线
与直线 交于
交于 ,
, 两点,且
两点,且 ,求
,求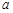 的值.
的值.
(1)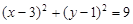 (2)
(2)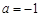
解析试题分析:解:(Ⅰ)设⊙ 的半径为
的半径为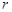 ,由题意可知
,由题意可知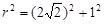 ,得
,得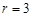 .
.
所以⊙ 的方程为
的方程为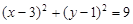 . ………………………4分
. ………………………4分
(Ⅱ)设A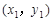 ,B
,B ,
,
联立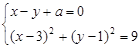 ,得
,得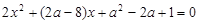 . ………………………6分
. ………………………6分
由已知可得,判别式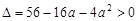 .
.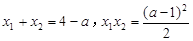 ………………………7分
………………………7分
由于OA⊥OB,可得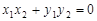 , ………………………9分
, ………………………9分
又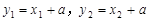 ,所以
,所以 ………………………10分
………………………10分
所以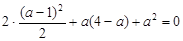
解得 ,满足
,满足 , ………………………11分
, ………………………11分
所以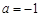 ………………………12分
………………………12分
考点:本试题考查了圆的方程。
点评:解决该试题的关键是根据圆心和半径的关系式来得到圆的方程,同时能联立方程组,求解相交点的坐标关系式,结合垂直关系,运用向量的数量积为零来得到参数的方程,求解得到结论,属于中档题。

练习册系列答案
相关题目
 ,圆
,圆 ,动圆
,动圆 与已知两圆都外切.
与已知两圆都外切. 的方程(2)直线
的方程(2)直线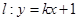 与点
与点 、
、 ,
, 的中垂线与
的中垂线与 轴交于点
轴交于点 ,求点
,求点 被圆
被圆 所截得的弦长.
所截得的弦长.  过点
过点 ,且与直线
,且与直线 相切于点
相切于点 .
.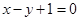 对称的圆
对称的圆 的方程.
的方程. ,过原点
,过原点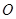 的直线
的直线 与圆
与圆 相交于
相交于 两点
两点 的长为
的长为 ,求直线
,求直线 为定值。
为定值。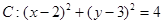 ,直线
,直线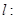
 ,
,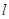 与圆
与圆 恒相交;
恒相交; 时,过圆
时,过圆 作圆的切线
作圆的切线 交直线
交直线 点,
点, 为圆
为圆 的取值范围;
的取值范围; .
. 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求 的取值范围.
的取值范围. 上,与
上,与 轴相切,且被直线
轴相切,且被直线 截得弦长为
截得弦长为 的圆的方程.
的圆的方程.  的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与
轴上,圆心的横坐标是整数,且与 相切.
相切.
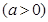 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数