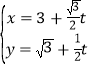题目内容
【题目】已知双曲线![]() 的右顶点为
的右顶点为![]() , 以
, 以![]() 为圆心的圆与双曲线
为圆心的圆与双曲线![]() 的某一条渐近线交于两点
的某一条渐近线交于两点![]() .若
.若![]() ,且
,且![]() (其中
(其中![]() 为原点),则双曲线
为原点),则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
设双曲线的一条渐近线方程为![]() x,A(a,0),P(m,
x,A(a,0),P(m,![]() ),(m>0),由向量共线的坐标表示,可得Q的坐标,求得弦长|PQ|,运用中点坐标公式,可得PQ的中点坐标,由两直线垂直的条件:斜率之积为﹣1,可得m
),(m>0),由向量共线的坐标表示,可得Q的坐标,求得弦长|PQ|,运用中点坐标公式,可得PQ的中点坐标,由两直线垂直的条件:斜率之积为﹣1,可得m![]() ,r
,r![]() ,运用圆的弦长公式计算即可得到a,b的关系,再由离心率公式计算即可得到所求值.
,运用圆的弦长公式计算即可得到a,b的关系,再由离心率公式计算即可得到所求值.
解:设双曲线的一条渐近线方程
为y![]() x,A(a,0),
x,A(a,0),
P(m,![]() ),(m>0),
),(m>0),
由![]() 3
3![]() ,可得Q(3m,
,可得Q(3m,![]() ),
),
圆的半径为r=|PQ|![]() 2m
2m![]() ,
,
PQ的中点为H(2m,![]() ),
),
由AH⊥PQ,可得![]() ,
,
解得m![]() ,r
,r![]() .
.
A到渐近线的距离为d![]() ,
,
则|PQ|=2![]() r,
r,
即为d![]() r,即有
r,即有![]()
![]() .
.
可得![]() ,
,
e![]() .
.
另解:可得△PAQ为等边三角形,
设OP=x,可得
设M为PQ的中点,可得PM=x,AM![]() x,
x,
tan∠MOA![]() ,
,
则e![]() .
.
故选:C.

练习册系列答案
相关题目