写出($\frac{1}{2}$+$\frac{1}{2}$)n的展开式．题目和参考答案——青夏教育精英家教网—

题目内容

6．写出（$\frac{1}{2}$+$\frac{1}{2}$）ⁿ的展开式．

分析由条件利用二项式定理把（$\frac{1}{2}$+$\frac{1}{2}$）ⁿ展开，可得结论．

解答解：写出（$\frac{1}{2}$+$\frac{1}{2}$）ⁿ的展开式为（$\frac{1}{2}$+$\frac{1}{2}$）ⁿ=${C}_{n}^{0}•（\frac{1}{2}）^{n}$+${C}_{n}^{1}•（\frac{1}{2}）^{n}$+…+${C}_{n}^{n}•（\frac{1}{2}）^{n}$．

点评本题主要考查二项式定理的应用，二项展开式的通项公式，属于基础题．

练习册系列答案

5．用多种方法求函数y=2x+$\sqrt{x-1}$最小值．（换元法或单调性）

14．求（x-1）⁹的展开式中系数最大的项．

1．求抛物线y²=4（x+1）及y²=4（1-x）所围成图形的面积．

11．设0＜x＜1，0＜y＜1，且x≠y，则x+y，2$\sqrt{xy}$，x²+y²，2xy中，最大的一个是（　　）

x²+y²

18．将（x+y+z+k）¹²展开式为多项式，经合并后共有多少个不同的项？

15．已知数列{a_n}满足a_n+1+2a_n=0，且a₁=2，则它的通项公式为a_n=（-1）^n-1•2ⁿ．

16．

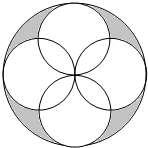如图，用4个半径为1的小圆去覆盖一个半径为2的大圆，在大圆内随机取一点，则此点取自阴影部分的概率是$\frac{1}{2}-\frac{1}{π}$．

试题分类