题目内容
15.已知数列{an}满足an+1+2an=0,且a1=2,则它的通项公式为an=(-1)n-1•2n.分析 由an+1+2an=0得到数列{an}是等比数列,结合等比数列的通项公式进行求解即可.
解答 解:∵an+1+2an=0,
∴an+1=-2an,
即数列{an}是公比q=-2的等比数列,
首项a1=2,
∴它的通项公式为an=a1qn-1=2•(-2)n-1=(-1)n-1•2n.
故答案为:an=(-1)n-1•2n.
点评 本题主要考查等比数列通项公式的求解,根据条件判断数列是等比数列是解决本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7.在约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{y+x≤4}\\{y+2x≤s}\end{array}\right.$下,当2≤s≤8时,目标函数z=3x+2y的最大值的变化范围是( )
| A. | [3,12] | B. | [4,12] | C. | [3,8] | D. | [6,12] |
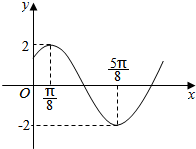 已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示:
已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示: