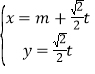题目内容
【题目】已知斜率为1的直线与抛物线![]() 交于
交于![]() 两点,
两点,![]() 中点的横坐标为2.
中点的横坐标为2.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,
,![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .除
.除![]() 以外,直线
以外,直线![]() 与
与![]() 是否有其它公共点?请说明理由.
是否有其它公共点?请说明理由.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)设点A,B坐标,将A,B坐标代入曲线C的方程,利用点差法计算即可得到p值;
(2)先求![]() 坐标,得到直线MH方程,与抛物线方程联立,利用判别式可得结论.
坐标,得到直线MH方程,与抛物线方程联立,利用判别式可得结论.
(1)设 ![]() ,
,![]() ,
,![]() 直线的斜率为
直线的斜率为![]() ,又因为
,又因为![]() ,
,![]() 都在曲线
都在曲线![]() 上,
上,
所以![]() ①
① ![]() ②
②
-得![]() ,
,
由已知条件![]() 得
得![]() ,得
,得![]() ,
,
所以抛物线![]() 的方程是
的方程是![]() .
.
(2)由题意,可知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,
,
从而可得直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程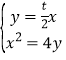 ,
,
解得![]() ,
,![]() .依题意,点
.依题意,点![]() 的坐标为
的坐标为![]() ,由于
,由于![]() ,
,![]() ,可得直线
,可得直线![]() 的方程为
的方程为![]() ,
,
联立方程![]() ,整理得
,整理得![]() ,
,
则![]() ,从而可知
,从而可知![]() 和
和![]() 只有一个公共点
只有一个公共点![]() .
.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品;当
时,产品为二等品;当![]() 时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
甲生产线生产的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
乙生产线产生的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
|
频数 | 10 | 15 | 25 | 30 | 20 |
(1)若从乙生产线生产的产品中有放回地随机抽取3件,求至少抽到2件三等品的概率;
(2)若该产品的利润率![]() 与质量指标值
与质量指标值![]() 满足关系:
满足关系: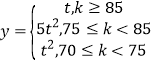 ,其中
,其中![]() ,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.
,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.