题目内容
【题目】在直角坐标系xOy中,曲线C:![]() 与直线l:
与直线l:![]() 交于M,N两点.
交于M,N两点.
![]() 当
当![]() 时,求
时,求![]() 的面积的取值范围;
的面积的取值范围;
![]() 轴上是否存在点P,使得当k变动时,总有
轴上是否存在点P,使得当k变动时,总有![]() ?若存在,求以线段OP为直径的圆的方程;若不存在,请说明理由.
?若存在,求以线段OP为直径的圆的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)联立直线的方程和抛物线的方程,写出韦达定理,利用弦长公式求得![]() ,用点到直线的距离公式求得
,用点到直线的距离公式求得![]() 到直线的距离,由此可求得三角形
到直线的距离,由此可求得三角形![]() 面积的表达式.再利用
面积的表达式.再利用![]() 的取值范围求得面积的取值范围.(2)设出
的取值范围求得面积的取值范围.(2)设出![]() 点的坐标,写出直线
点的坐标,写出直线![]() 的斜率,然后相加,利用(1)的韦达定理条件化简,并令斜率和为零,由此求得
的斜率,然后相加,利用(1)的韦达定理条件化简,并令斜率和为零,由此求得![]() 点的坐标,进而求得以
点的坐标,进而求得以![]() 为直径的圆的方程.
为直径的圆的方程.
(1)将![]() 代入
代入![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
从而![]() .
.
因为![]() 到
到![]() 的距离为
的距离为![]() ,
,
所以![]() 的面积
的面积![]() .
.
因为![]() ,所以
,所以![]() .
.
(2)存在符合题意的点,证明如下:
设![]() 为符合题意的点,直线
为符合题意的点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
从而![]()
![]()
![]() .
.
当![]() 时,有
时,有![]() ,则直线
,则直线![]() 的倾斜角与直线
的倾斜角与直线![]() 的倾斜角互补,
的倾斜角互补,
故![]() ,所以点
,所以点![]() 符合题意.
符合题意.
故以线段![]() 为直径的圆的方程为
为直径的圆的方程为![]() .
.

【题目】已知斜率为1的直线与抛物线![]() 交于
交于![]() 两点,
两点,![]() 中点的横坐标为2.
中点的横坐标为2.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,
,![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .除
.除![]() 以外,直线
以外,直线![]() 与
与![]() 是否有其它公共点?请说明理由.
是否有其它公共点?请说明理由.
【题目】某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了![]() 名员工进行问卷调查,其中
名员工进行问卷调查,其中![]() 的员工工作积极.经汇总调查,这
的员工工作积极.经汇总调查,这![]() 名员工是否支持企业改革的调查得分(百分制)如茎叶图(图
名员工是否支持企业改革的调查得分(百分制)如茎叶图(图![]() )所示.调查评价标准指出:调查得分不低于
)所示.调查评价标准指出:调查得分不低于![]() 分者为积极支持企业改革,调查得分低于70分者不太赞成企业改革.
分者为积极支持企业改革,调查得分低于70分者不太赞成企业改革.
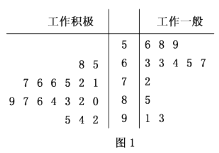
(1)根据以上资料完成下面的![]() 列联表,结合数据能否有
列联表,结合数据能否有![]() 的把握认为员工的工作积极性与“是否积极支持企业改革”是有关的,并回答人力资源部的研究项目.
的把握认为员工的工作积极性与“是否积极支持企业改革”是有关的,并回答人力资源部的研究项目.
积极支持企业改革 | 不太赞成企业改革 | 总计 | |
工作积极 | |||
工作一般 | |||
总计 |
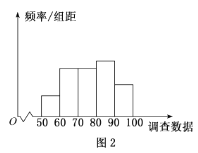
(2)现将![]() 名员工的调查得分分为如下
名员工的调查得分分为如下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 其频率分布直方图如图
其频率分布直方图如图![]() 所示,这
所示,这![]() 名员工的调查数据得分的平均值可由茎叶图得到,记为
名员工的调查数据得分的平均值可由茎叶图得到,记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),
(同一组中的数据用该组区间的中点值作代表),![]() 与
与![]() 的误差值在
的误差值在![]() 以内,可以由
以内,可以由![]() 代替
代替![]() ,能否由
,能否由![]() 代替
代替![]() ?(提示:
?(提示:![]() 名员工的调查数据得分的和
名员工的调查数据得分的和![]() )
)
(3)该企业人力资源部从![]() 分以上的员工中任选
分以上的员工中任选![]() 名员工进行座谈,则所选员工的分数超过
名员工进行座谈,则所选员工的分数超过![]() 分的人数的数学期望是多少?
分的人数的数学期望是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附: .
.


