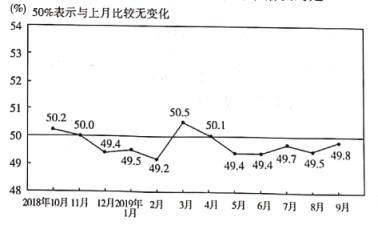
题目内容
【题目】如图,![]() 是南北方向的一条公路,
是南北方向的一条公路,![]() 是北偏东
是北偏东![]() 方向的一条公路,某风景区的一段边界为曲线
方向的一条公路,某风景区的一段边界为曲线![]() .为方便游客光,拟过曲线
.为方便游客光,拟过曲线![]() 上的某点分别修建与公路
上的某点分别修建与公路![]() ,
,![]() 垂直的两条道路
垂直的两条道路![]() ,
,![]() ,且
,且![]() ,
,![]() 的造价分别为5万元
的造价分别为5万元![]() 百米,40万元
百米,40万元![]() 百米,建立如图所示的直角坐标系
百米,建立如图所示的直角坐标系![]() ,则曲线符合函数
,则曲线符合函数![]() 模型,设
模型,设![]() ,修建两条道路
,修建两条道路![]() ,
,![]() 的总造价为
的总造价为![]() 万元,题中所涉及的长度单位均为百米.
万元,题中所涉及的长度单位均为百米.
(1)求![]() 解析式;
解析式;
(2)当![]() 为多少时,总造价
为多少时,总造价![]() 最低?并求出最低造价.
最低?并求出最低造价.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,总造价最低,最低造价为30万元.
时,总造价最低,最低造价为30万元.
【解析】
(1)求出![]() 的坐标,直线
的坐标,直线![]() 的方程,点
的方程,点![]() 到直线
到直线![]() 的距离,即可求
的距离,即可求![]() 解析式;
解析式;
(2)利用导数的方法最低造价.
解:(1)在如图所示的直角坐标系中,因为曲线![]() 的方程为
的方程为![]() ,
,
所以点![]() 坐标为
坐标为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为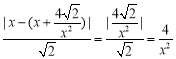 ,
,
又![]() 的造价为5万元
的造价为5万元![]() 百米,
百米,![]() 的造价为40万元
的造价为40万元![]() 百米.
百米.
则两条道路总造价为![]() .
.
(2)因为![]() ,
,
所以![]() ,
,
令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
| 4 |
|
|
| 0 |
|
| 单调递减 | 极小值 | 单调递增 |
所以当![]() 时,函数
时,函数![]() 有最小值,最小值为
有最小值,最小值为![]() .
.
答:(1)两条道路![]() ,
,![]() 总造价
总造价![]() 为
为![]() ;
;
(2)当![]() 时,总造价最低,最低造价为30万元.
时,总造价最低,最低造价为30万元.

练习册系列答案
相关题目