题目内容
(本题满分14分)
已知函数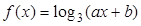 的图象经过点
的图象经过点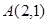 和
和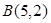 ,记
,记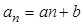 (
( )
)
(1)求数列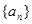 的通项公式;
的通项公式;
(2)设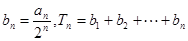 ,若
,若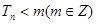 ,求
,求 的最小值;
的最小值;
(3)求使不等式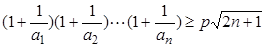 对一切
对一切 均成立的最大实数
均成立的最大实数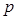 .
.
(1)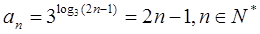 ;
;
(2) ; (3)
; (3)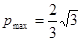 .
.
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
(本题满分14分)
已知函数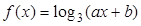 的图象经过点
的图象经过点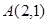 和
和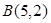 ,记
,记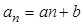 (
( )
)
(1)求数列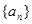 的通项公式;
的通项公式;
(2)设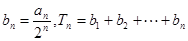 ,若
,若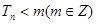 ,求
,求 的最小值;
的最小值;
(3)求使不等式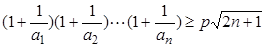 对一切
对一切 均成立的最大实数
均成立的最大实数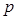 .
.
(1)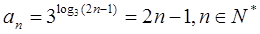 ;
;
(2) ; (3)
; (3)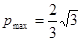 .
.
解析

 阅读快车系列答案
阅读快车系列答案